
【题目】如图所示,在平面直角坐标系中,一次函数![]() 与反比例函数
与反比例函数![]() 交于
交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,作
,作![]() 轴,垂足为
轴,垂足为![]() ,已知
,已知![]() ,
,![]() .
.
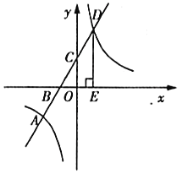
(1)求一次函数与反比例函数的解析式;
(2)连接![]() 、
、![]() ,在
,在![]() 轴取点
轴取点![]() ,使
,使![]() 与
与![]() 面积相等,求点
面积相等,求点![]() 坐标.
坐标.
【答案】(1)![]() ;
;![]() ;(2)(2,0)或(-4,0).
;(2)(2,0)或(-4,0).
【解析】
(1)根据题意,结合直角三角形求解,得出点B、C的坐标代入一次函数![]() ,可得直线解析式,进而求出点D,可求出反比例函数
,可得直线解析式,进而求出点D,可求出反比例函数![]() 的解析式即可;
的解析式即可;
(2)联立方程组求出点A,进而求出![]() 的面积,根据
的面积,根据![]() 与
与![]() 面积相等列出关于底边长的一次方程求解即可.
面积相等列出关于底边长的一次方程求解即可.
(1)在Rt△COB中,OB=1,![]() ,
,
∴CO=![]() ,
,
将点B(-1,0),点C(0,![]() )代入
)代入![]() ,得
,得
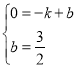 ,
,
解得![]() ,
,
∴![]() ,
,
∵CO⊥x轴,DE⊥x轴,OB=OE,
∴CO为△BED的中位线,
∴DE=2CO=3,
∴点D的坐标为(1,3),
∴将(1,3)代入![]() ,得m=3,
,得m=3,
∴![]() ,
,
故答案为:![]() ;
;![]() ;
;
(2)连接DO、AO,
将![]() 与
与![]() 联立方程组,得
联立方程组,得
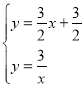 ,
,
解得![]() 或
或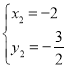 ,
,
∴点A坐标为(-2,![]() ),D(1,3),
),D(1,3),
∴![]() ,
,
设△CBF的底边长为a,
可得:![]() ,
,
解得:a=3,
∴点F的坐标为(-1+3,0),(-1-3,0),
即点F的坐标为(2,0)或(-4,0),
故答案为:(2,0)或(-4,0).



 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】问题提出
(1)如图①,在矩形ABCD中,AB=2AD,E为CD的中点,则∠AEB ∠ACB(填“>”“<”“=”);
问题探究
(2)如图②,在正方形ABCD中,P为CD边上的一个动点,当点P位于何处时,∠APB最大?并说明理由;
问题解决
(3)如图③,在一幢大楼AD上装有一块矩形广告牌,其侧面上、下边沿相距6米(即AB=6米),下边沿到地面的距离BD=11.6米.如果小刚的睛睛距离地面的高度EF为1.6米,他从远处正对广告牌走近时,在P处看广告效果最好(视角最大),请你在图③中找到点P的位置,并计算此时小刚与大楼AD之间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在春节来临之际,小杨的服装小店用2500元购进了一批时尚围巾,上市后很快售完,小杨又用8400元购进第二批这种围巾,所购数量是第一批购进数量的3倍,但每条围巾的进价多了3元.
(1)小杨两次共购进这种围巾多少条?
(2)如果这两批围巾每条的售价相同,且全部售完后总利润率不低于20%,那么每条围巾的售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家具生产厂生产某种配套桌椅(一张桌子,两把椅子),已知每块板材可制作桌子![]() 张或椅子
张或椅子![]() 把,现计划用
把,现计划用![]() 块这种板材生产一批桌椅(不考虑板材的损耗,恰好配套),设用
块这种板材生产一批桌椅(不考虑板材的损耗,恰好配套),设用![]() 块板材做椅子,用
块板材做椅子,用![]() 块板材做桌子,则下列方程组正确的是( )
块板材做桌子,则下列方程组正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市拟于中秋节前![]() 天里销售某品牌月饼,其进价为
天里销售某品牌月饼,其进价为![]() 元/
元/![]() .设第
.设第![]() 天的销售价格为
天的销售价格为![]() (元/
(元/![]() )销售量为
)销售量为![]() .该超市根据以往的销售经验得出以下的销售规律:①与
.该超市根据以往的销售经验得出以下的销售规律:①与![]() 满足一次函数关系,且当
满足一次函数关系,且当![]() 时,
时,![]() ;
;![]() 时,
时,![]() .②
.②![]() 与
与![]() 的关系为
的关系为![]() .
.
(1)![]() 与
与![]() 的关系式为________;
的关系式为________;
(2)当![]() 时,求第几天的销售利润
时,求第几天的销售利润![]() (元)最大?最大利润为多少?
(元)最大?最大利润为多少?
(3)若在当天销售价格的基础上涨![]() 元/
元/![]() ,在第
,在第![]() 天至
天至![]() 天销售利润最大值为
天销售利润最大值为![]() 元,求
元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司投入研发费用40万元(40万元只计入第一年成本),成功研发出一种产品.公司按订单生产(产量=销售量),第一年该产品正式投产后,生产成本为4元/件.此产品年销售量y(万件)与售价x(元件)之间满足函数关系式y=﹣x+20.
(1)求这种产品第一年的利润W(万元)与售价x(元件)满足的函数关系式;
(2)该产品第一年的利润为24万元,那么该产品第一年的售价是多少?
(3)第二年,该公司将第一年的利润24万元(24万元只计入第二年成本)再次投入研发,使产品的生产成本降为3元/件.为保持市场占有率,公司规定第二年产品售价不超过第一年的售价,另外受产能限制,销售量无法超过10万件.请计算该公司第二年的利润W2至少为多少万元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com