
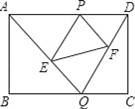
��ͼ����֪����ABCD�ı߳�AB=2��BC=3����P��AD��һ���㣨��P����A��D���㣩��Q��BC������һ�㣬����AQ��DQ����P��PE��DQ��AQ��E����PF��AQ��DQ��F��
��1����գ���APE�ס�����������������DPF�ס���������������
��2����AP�ij�Ϊx����APE�����Ϊy1����DPF�����Ϊy2���ֱ����y2��y1����x�ĺ�����ϵʽ��
��3���ڱ�AD���Ƿ���������ĵ�P��ʹ��PEF�����Ϊ
 �����������x��ֵ������������˵�����ɣ�
�����������x��ֵ������������˵�����ɣ�

��
�����㡿�������ۺ��⣮
����������1���������������ε��ж�����֤�����ɣ�
��2���������������ε�����ȵ������Ʊȵ�ƽ�����㼴�ɣ�
��3�����������г�һԪ���η��̣��ⷽ�̼��ɣ�
����𡿽⣺��1����PE��DQ��
���APE�ס�ADQ��
��PF��AQ��
���DPF�ס�DAQ��
�ʴ�Ϊ��ADQ��DAQ��
��2�����ADQ�����Ϊy��
��S=
 ��AD��AB=3��
��AD��AB=3��
�ɡ�APE�ס�ADQ�ã�y1��y=��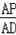
 ��2=
��2=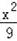
 ��
��
��y1=
 x2��
x2��
ͬ���ɵ�y2=
 ��3��x��2��
��3��x��2��
��3����PE��DQ��PF��AQ��
���ı���PEQF��ƽ���ı��Σ�
���PEF���������
 ��y��y1��y2��=��
��y��y1��y2��=��
 x2+x
x2+x
��y=
 ʱ����
ʱ����
 x2+x=
x2+x=
 ��
��
��������̵ã�x=
 ��
��
�����������ĵ�P����x=
 ʱ�ǡ�PEF�����Ϊ
ʱ�ǡ�PEF�����Ϊ
 ��
��
�����������⿼��������������ε�֪ʶ���ۺ����ã��������������ε��ж����������ʶ����ǽ���Ĺؼ���
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ���������ABCDE�У���A+��B+��E=300�㣬DP��CP�ֱ�ƽ�֡�EDC����BCD�����P�Ķ����ǣ�������
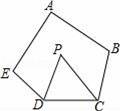

A��60�� B��65�� C��55�� D��50��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��3��3�ķ���ֽ�У���A��B��C��D��E��F�ֱ�λ����ͼ��ʾ��С�����εĶ����ϣ�
��1����A��D��E��F�ĸ���������ȡһ�㣬����ȡ����һ�㼰��B��CΪ���㻭�����Σ��������������ǵ��������εĸ�������������������
��2����A��D��E��F�ĸ������Ⱥ�����ȡ������ͬ�ĵ㣬����ȡ�������㼰��B��CΪ���㻭�ı��Σ��������ı�����ƽ���ı��εĸ�����������������������״ͼ���б�����⣩��


��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����x��һԪ���η��̣�x��2����x��3��=m����������ȵ�ʵ����x1��x2����m��ȡֵ��Χ����x1��x2�����ʽx1x2��x1��x2+1=0����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����x2��3x��5=0�ĸ�������ǣ�������
A������������ȵ�ʵ���� B����������ȵ�ʵ����
C��û��ʵ���� D����ȷ���Ƿ���ʵ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
ij���½��ɵ�һ��¥������8�㣬���ӵļ۸�y��Ԫ/ƽ���ף���¥����x��¥���ı仯���仯����֪�㣨x��y������һ�����κ�����ͼ���ϣ���ͼ������6¥���ӵļ۸�Ϊ������������Ԫ/ƽ���ף�
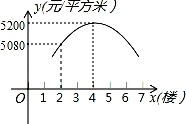
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com