
关于x的一元二次方程(x﹣2)(x﹣3)=m有两个不相等的实数根x1,x2,求m的取值范围;若x1,x2满足等式x1x2﹣x1﹣x2+1=0,求m的值.
【考点】根的判别式;根与系数的关系.
【分析】原方程可化为x2﹣5x+6﹣m=0,于是得到△=b2﹣4ac=25﹣24+4m=1+4m,根据方程(x﹣2)(x﹣3)=m有两个不相等的实数根,得到△>0,求得m>﹣
 根据根与系数的关系得到x1+x2=5,x1x2=6﹣m解方程即可得到结论.
根据根与系数的关系得到x1+x2=5,x1x2=6﹣m解方程即可得到结论.
【解答】解:原方程可化为x2﹣5x+6﹣m=0,
△=b2﹣4ac=25﹣24+4m=1+4m,
∵方程(x﹣2)(x﹣3)=m有两个不相等的实数根,
∴△>0,
∴1+4m>0,
∴m>﹣

∵x1+x2=5,x1x2=6﹣m
∴5﹣6+m+1=0,
∴m=0.
【点评】本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2﹣4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.


科目:初中数学 来源: 题型:
等边三角形ABC中,BC=6,D、E是边BC上两点,且BD=CE=1,点P是线段DE上的一个动点,过点P分别作AC、AB的平行线交AB、AC于点M、N,连接MN、AP交于点G,则点P由点D移动到点E的过程中,线段BG扫过的区域面积为 .


查看答案和解析>>
科目:初中数学 来源: 题型:
“服务他人,提升自我”,七一学校积极开展志愿者服务活动,来自初三的5名同学(3男两女)成立了“交通秩序维护”小分队,若从该小分队中任选两名同学进行交通秩序维护,则恰好是一男一女的概率是( )
A.
 B.
B.
 C.
C.
 D.
D.

查看答案和解析>>
科目:初中数学 来源: 题型:
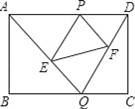
如图,已知矩形ABCD的边长AB=2,BC=3,点P是AD上一动点(点P异于A、D两点),Q是BC上任意一点,连结AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.
(1)填空:△APE∽△ ,△DPF∽△ .
(2)设AP的长为x,△APE的面积为y1,△DPF的面积为y2,分别求出y2和y1关于x的函数关系式;
(3)在边AD上是否存在这样的点P,使△PEF的面积为
 ?若存在求出x的值;若不存在请说明理由.
?若存在求出x的值;若不存在请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,△ABC中,D、E是BC边上的点,BD:DE:EC=3:2:1,M在AC边上,CM:MA=1:2,BM交AD,AE于H,G,则BH:HG:GM等于( )
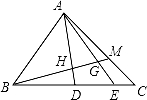
A.3:2:1 B.5:3:1 C.25:12:5 D.51:24:10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com