
等边三角形ABC中,BC=6,D、E是边BC上两点,且BD=CE=1,点P是线段DE上的一个动点,过点P分别作AC、AB的平行线交AB、AC于点M、N,连接MN、AP交于点G,则点P由点D移动到点E的过程中,线段BG扫过的区域面积为 .


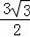
 .
.
【考点】轨迹.
【分析】求出四边形AMPN是平行四边形,根据平行四边形的对角线互相平分可得G是AP的中点,然后判断出点G的运动路线是△APP′的中位线,根据三角形的中位线平行于第三边并且等于第三边的一半求出GG′,再根据等边三角形的性质求出△BGG′的底边GG′上的高,然后根据三角形的面积公式列式计算即可得解.
【解答】解:∵PM∥AC,PN∥AB,
∴四边形AMPN是平行四边形,
∵MN与AP相交于点G,
∴G是AP的中点,
∴如图点G的运动路线是△APP′的中位线,
∵BC=6,BD=CE=1,
∴GG′=
 =2,
=2,
∵BC=6,
∴△BGG′的底边GG′上的高=
 ×(6×
×(6×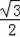
 )=
)=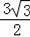
 ,
,
∴线段BG扫过的区域面积=
 ×2×
×2×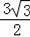
 =
=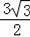
 .
.
故答案为: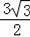
 .
.
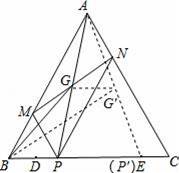

【点评】本题考查了点的轨迹,等边三角形的性质,平行四边形的判定与性质,三角形的中位线平行于第三边并且等于第三边的一半,难点在于确定出点G的运动轨迹从而确定出BG扫过的区域是三角形.


科目:初中数学 来源: 题型:
若点M(﹣2,y1),N(﹣1,y2),P(8,y3)在抛物线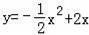
 上,则下列结论正确的是( )
上,则下列结论正确的是( )
A.y1<y2<y3 B.y2<y1<y3 C.y3<y1<y2 D.y1<y3<y2
查看答案和解析>>
科目:初中数学 来源: 题型:
在3×3的方格纸中,点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上.
(1)从A、D、E、F四个点中任意取一点,以所取的这一点及点B、C为顶点画三角形,则所画三角形是等腰三角形的概率是 ;
(2)从A、D、E、F四个点中先后任意取两个不同的点,以所取的这两点及点B、C为顶点画四边形,求所画四边形是平行四边形的概率是 (用树状图或列表法求解).


查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,平面直角坐标系中,等腰直角三角形的直角边BC在x轴正半轴上滑动,点C的坐标为(t,0),直角边AC=4,经过O,C两点做抛物线y1=ax(x﹣t)(a为常数,a>0),该抛物线与斜边AB交于点E,直线OA:y2=kx(k为常数,k>0)
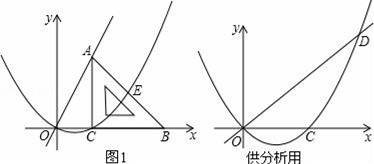

(1)填空:用含t的代数式表示点A的坐标及k的值:A ,k= ;
(2)随着三角板的滑动,当a=
 时:
时:
①请你验证:抛物线y1=ax(x﹣t)的顶点在函数y=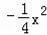
 的图象上;
的图象上;
②当三角板滑至点E为AB的中点时,求t的值;
(3)直线OA与抛物线的另一个交点为点D,当t≤x≤t+4,|y2﹣y1|的值随x的增大而减小,当x≥t+4时,|y2﹣y1|的值随x的增大而增大,求a与t的关系式及t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
关于x的一元二次方程(x﹣2)(x﹣3)=m有两个不相等的实数根x1,x2,求m的取值范围;若x1,x2满足等式x1x2﹣x1﹣x2+1=0,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com