
ЁОЬтФПЁПЖЈвхЃК
Ъ§бЇЛюЖЏПЮЩЯЃЌРюРЯЪІИјГіШчЯТЖЈвхЃКШчЙћвЛИіШ§НЧаЮгавЛБпЩЯЕФжаЯпЕШгкетЬѕБпЕФвЛАыЃЌФЧУДГЦШ§НЧаЮЮЊЁАжЧЛлШ§НЧаЮЁБ.

РэНтЃК
ЂХШчЭМ![]() ЃЌвбжЊ
ЃЌвбжЊ![]() ЪЧЁб
ЪЧЁб![]() ЩЯСНЕуЃЌЧыдкдВЩЯевГіТњзуЬѕМўЕФЕу
ЩЯСНЕуЃЌЧыдкдВЩЯевГіТњзуЬѕМўЕФЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЮЊЁАжЧЛлШ§НЧаЮЁБЃЈЛГіЕу
ЮЊЁАжЧЛлШ§НЧаЮЁБЃЈЛГіЕу![]() ЕФЮЛжУЃЌБЃСєзїЭМКлМЃЃЉЃЛ
ЕФЮЛжУЃЌБЃСєзїЭМКлМЃЃЉЃЛ
ЂЦШчЭМ![]() ЃЌдке§ЗНаЮ
ЃЌдке§ЗНаЮ![]() жаЃЌ
жаЃЌ![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]() ЪЧ
ЪЧ![]() ЩЯвЛЕуЃЌЧв
ЩЯвЛЕуЃЌЧв![]() ЃЌЪдХаЖЯ
ЃЌЪдХаЖЯ![]() ЪЧЗёЮЊЁАжЧЛлШ§НЧаЮЁБЃЌВЂЫЕУїРэгЩЃЛ
ЪЧЗёЮЊЁАжЧЛлШ§НЧаЮЁБЃЌВЂЫЕУїРэгЩЃЛ
дЫгУЃК
ЂЧШчЭМ![]() ЃЌдкЦНУцжБНЧзјБъЯЕ
ЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЁб
жаЃЌЁб![]() ЕФАыОЖЮЊ
ЕФАыОЖЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЪЧжБЯп
ЪЧжБЯп![]() ЩЯЕФвЛЕуЃЌШєдкЁб
ЩЯЕФвЛЕуЃЌШєдкЁб![]() ЩЯДцдквЛЕу
ЩЯДцдквЛЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЮЊЁАжЧЛлШ§НЧаЮЁБЃЌЕБЦфУцЛ§ШЁЕУзюаЁжЕЪБЃЌжБНгаДГіДЫЪБЕу
ЮЊЁАжЧЛлШ§НЧаЮЁБЃЌЕБЦфУцЛ§ШЁЕУзюаЁжЕЪБЃЌжБНгаДГіДЫЪБЕу![]() ЕФзјБъ.
ЕФзјБъ.
ЁОД№АИЁПЃЈ1ЃЉЯъМћНтЮіЃЛЃЈ2ЃЉЯъМћНтЮіЃЛЃЈ3ЃЉPЕФзјБъЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЌЃЈ
ЃЉЃЌЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉСЌНсAOВЂЧвбгГЄНЛдВгкC1ЃЌСЌНсBOВЂЧвбгГЄНЛдВгкC2ЃЌМДПЩЧѓНтЃЛЃЈ2ЃЉЩше§ЗНаЮЕФБпГЄЮЊ4aЃЌБэЪОГіDF=CFвдМАECЁЂBEЕФГЄЃЌШЛКѓИљОнЙДЙЩЖЈРэСаЪНБэЪОГіAF2ЁЂEF2ЁЂAE2ЃЌдйИљОнЙДЙЩЖЈРэФцЖЈРэХаЖЈЁїAEFЪЧжБНЧШ§НЧаЮЃЌгЩжБНЧШ§НЧаЮЕФаджЪПЩЕУЁїAEFЮЊЁАжЧЛлШ§НЧаЮЁБЃЛЃЈ3ЃЉИљОнЁАжЧЛлШ§НЧаЮЁБЕФЖЈвхПЩЕУЁїOPQЮЊжБНЧШ§НЧаЮЃЌИљОнЬтвтПЩЕУвЛЬѕжБНЧБпЮЊ1ЃЌЕБаББпзюЖЬЪБЃЌСэвЛЬѕжБНЧБпзюЖЬЃЌдђУцЛ§ШЁЕУзюаЁжЕЃЌгЩДЙЯпЖЮзюЖЬПЩЕУаББпзюЖЬЮЊ3ЃЌИљОнЙДЙЩЖЈРэПЩЧѓСэвЛЬѕжБНЧБпЃЌдйИљОнШ§НЧаЮУцЛ§ПЩЧѓаББпЕФИпЃЌМДЕуPЕФКсзјБъЃЌдйИљОнЙДЙЩЖЈРэПЩЧѓЕуPЕФзнзјБъЃЌДгЖјЧѓНтЃЎ
ЪдЬтНтЮіЃК
ЃЈ1ЃЉШчЭМ1ЫљЪОЃК
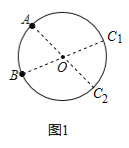
ЃЈ2ЃЉЁїAEFЪЧЗёЮЊЁАжЧЛлШ§НЧаЮЁБЃЌ
РэгЩШчЯТЃКЩше§ЗНаЮЕФБпГЄЮЊ4aЃЌ
ЁпEЪЧDCЕФжаЕуЃЌ
ЁрDE=CE=2aЃЌ
ЁпBCЃКFC=4ЃК1ЃЌ
ЁрFC=aЃЌBF=4aЉa=3aЃЌ
дкRtЁїADEжаЃЌAE2=ЃЈ4aЃЉ2+ЃЈ2aЃЉ2=20a2ЃЌ
дкRtЁїECFжаЃЌEF2=ЃЈ2aЃЉ2+a2=5a2ЃЌ
дкRtЁїABFжаЃЌAF2=ЃЈ4aЃЉ2+ЃЈ3aЃЉ2=25a2ЃЌ
ЁрAE2+EF2=AF2ЃЌ
ЁрЁїAEFЪЧжБНЧШ§НЧаЮЃЌ
ЁпаББпAFЩЯЕФжаЯпЕШгкAFЕФвЛАыЃЌ
ЁрЁїAEFЮЊЁАжЧЛлШ§НЧаЮЁБЃЛ
ЃЈ3ЃЉШчЭМ3ЫљЪОЃК
гЩЁАжЧЛлШ§НЧаЮЁБЕФЖЈвхПЩЕУЁїOPQЮЊжБНЧШ§НЧаЮЃЌ
ИљОнЬтвтПЩЕУвЛЬѕжБНЧБпЮЊ1ЃЌЕБаББпзюЖЬЪБЃЌСэвЛЬѕжБНЧБпзюЖЬЃЌдђУцЛ§ШЁЕУзюаЁжЕЃЌ
гЩДЙЯпЖЮзюЖЬПЩЕУаББпзюЖЬЮЊ3ЃЌ
гЩЙДЙЩЖЈРэПЩЕУPQ=![]() ЃЌ
ЃЌ
PM=1ЁС2![]() ЁТ3=
ЁТ3=![]() ЃЌ
ЃЌ
гЩЙДЙЩЖЈРэПЩЧѓЕУOM=![]() ЃЌ
ЃЌ
ЙЪЕуPЕФзјБъЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЌЃЈ
ЃЉЃЌЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ




| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖўДЮКЏЪ§y=ax2+bx+cЃЈaЁй0ЃЉЕФЭМЯѓШчЭМЫљЪОЃЌИљОнЭМЯѓНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉаДГіЗНГЬax2+bx+c=0ЕФСНИіИљЃЛ
ЃЈ2ЃЉаДГіВЛЕШЪНax2+bx+c<0ЕФНтМЏЃЛ
ЃЈ3ЃЉШєЗНГЬax2+bx+c+k=0гаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЌЧѓkЕФШЁжЕЗЖЮЇЃЎ
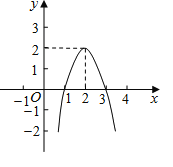
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
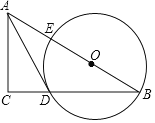
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЕуOдкаББпABЩЯЃЌвдOЮЊдВаФЃЌOBЮЊАыОЖзїдВЃЌЗжБ№гыBCЃЌABЯрНЛгкЕуDЃЌEЃЌСЌНсADЃЎвбжЊЁЯCAD=ЁЯB,
ЃЈ1ЃЉЧѓжЄЃКADЪЧЁбOЕФЧаЯпЃЎ
ЃЈ2ЃЉШєBC=8ЃЌtanB=![]() ЃЌЧѓЁбO ЕФАыОЖЃЎ
ЃЌЧѓЁбO ЕФАыОЖЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
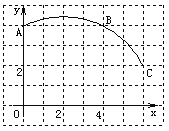
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮЭјИёЭМжаНЈСЂвЛжБНЧзјБъЯЕЃЌвЛЬѕдВЛЁОЙ§ЭјИёЕуAЁЂBЁЂCЃЌЧыЛиД№ЃК
ЃЈ1ЃЉИУдВЛЁЫљдкдВаФDЕуЕФзјБъЮЊ ЃЛ
ЃЈ2ЃЉЩШаЮDACЕФдВаФНЧЖШЪ§ЮЊ ЃЛ
ЃЈ3ЃЉШєЩШаЮDACЪЧФГвЛИідВзЖЕФВрУцеЙПЊЭМЃЌЧѓИУдВзЖЕФИпЃЎЃЈБЃСєИљКХЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигк![]() ЕФвЛдЊЖўДЮЗНГЬ
ЕФвЛдЊЖўДЮЗНГЬ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉШєДЫЗНГЬЕФвЛИіИљЮЊ1ЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЧѓжЄЃКВЛТл![]() ШЁКЮЪЕЪ§ЃЌДЫЗНГЬЖМгаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЎ
ШЁКЮЪЕЪ§ЃЌДЫЗНГЬЖМгаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНтЗНГЬ
(1)x2-7x+6=0
(2)(5x-1)2=3(5x-1)
(3) x2-4x-3=0 (гУХфЗНЗЈ)
(4) x2+4x+2=0(гУЙЋЪНЗЈ)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпyЃНx2+ax+bгыxжсНЛгкЕуAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЙ§ЕуDЃЈ0ЃЌ![]() ЃЉзїxжсЕФЦНааЯпНЛХзЮяЯпгкEЃЌFСНЕуЃЌЧѓEFЕФГЄЃЛ
ЃЉзїxжсЕФЦНааЯпНЛХзЮяЯпгкEЃЌFСНЕуЃЌЧѓEFЕФГЄЃЛ
ЃЈ3ЃЉЕБ![]() ЪБЃЌжБНгаДГіxЕФШЁжЕЗЖЮЇЪЧЁЁ ЁЁЃЎ
ЪБЃЌжБНгаДГіxЕФШЁжЕЗЖЮЇЪЧЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,дкRtЁїABCжа,ЁЯC=90ЁуЃЌAC=3ЃЌBC=4ЃЌЕуEЃЌFЗжБ№дкБпBCЃЌACЩЯЃЌбиEFЫљдкЕФжБЯпелЕўЁЯCЃЌЪЙЕуCЕФЖдгІЕуDЧЁКУТфдкБпABЩЯЃЌШєЁїEFCКЭЁїABCЯрЫЦЃЌдђADЕФГЄЮЊ___.
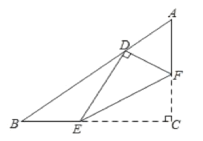
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФЗНГЬx2+ЃЈm+2ЃЉx+2m-1=0.
ЃЈ1ЃЉЧѓжЄЗНГЬгаСНИіВЛЯрЕШЕФЪЕЪ§Иљ.
ЃЈ2ЃЉЕБmЮЊКЮжЕЪБЃЌЗНГЬЕФСНИљЛЅЮЊЯрЗДЪ§ЃПВЂЧѓГіДЫЪБЗНГЬЕФНт.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com