
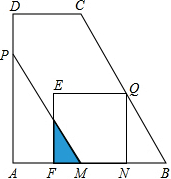
 ��ͼ��������ABCD�У�AB��CD����A=90�㣬AB=AD=10��CD=5������P�ӵ�A������������AD-DC��ÿ��4����λ���ٶ����C�˶�����Q�ӵ�B���������߶�BC��ÿ��$\sqrt{5}$����λ���ٶ����C�˶���P��Q����ͬʱ������������һ�㵽���յ�ʱ����һ��Ҳֹͣ�˶�������P��PM��BC��AB��M������Q��QN��AB��AB��N�����߶�QNΪһ����QN�������������QEFN�����˶�ʱ��Ϊt��s�����߶�PMɨ��ƽ�沿����������QEFN�ص����ֵ����ΪS��
��ͼ��������ABCD�У�AB��CD����A=90�㣬AB=AD=10��CD=5������P�ӵ�A������������AD-DC��ÿ��4����λ���ٶ����C�˶�����Q�ӵ�B���������߶�BC��ÿ��$\sqrt{5}$����λ���ٶ����C�˶���P��Q����ͬʱ������������һ�㵽���յ�ʱ����һ��Ҳֹͣ�˶�������P��PM��BC��AB��M������Q��QN��AB��AB��N�����߶�QNΪһ����QN�������������QEFN�����˶�ʱ��Ϊt��s�����߶�PMɨ��ƽ�沿����������QEFN�ص����ֵ����ΪS������ ��1��������֪������֤����PAM�ס�QNB�ס�CGB�����AM��FN��BN�ij�������AM+FN+BN=AB�����t��
��2�����P�˶�����Dʱ�����߶�PM������FE-EQ�ڵ�H��֤��H��E�غϣ�
��3�����������ͼ�Σ���ʾ���ص����ֵ����S�����������ϵʽ��
��4�����������ͼ��ֱ��д��ʱ��t��
��� �⣺��1����ͼ1����C��CG��AB��
��PM��BC��
���PMA=��CBA��
�ߡ�A=��QNB=��CGB=90�㣬
���PAM�ס�QNB�ס�CGB��
��$\frac{PA}{AM}$=$\frac{QN}{NB}$$\frac{CG}{GB}$=$\frac{10}{10-5}$=2��
��PA=4t��BQ=$\sqrt{5}$t��
��AM=2t��BN=t��QN=FN=2t��
������M��N����ʱ��AM+FN+BN=AB����2t+2t+t=10��
��ã�t=2��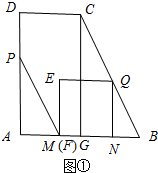
��2������P�˶�����Dʱ�����߶�PM������FE-EQ�ڵ�H��
��AP=AD=10����t=$\frac{5}{2}$��
��AM=5��BN=$\frac{5}{2}$��FN=5��
��FM=AM+BN+FN-AB=5+$\frac{5}{2}$+5-10=$\frac{5}{2}$��
��FH�ǡ�PAM����λ�ߣ�
��FH=$\frac{1}{2}$AP=5��
��EF=5��
��H��E�غϣ����߶�PM����E��
��3����M��N�غ�ʱ����ͼ�ڣ�CP=MB��
��CP=DC-DP=5-��4t-10������5-��4t-10��=t��
��ã�t=3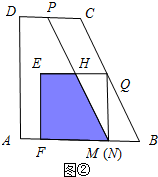
�ٵ�2��t��$\frac{5}{2}$ʱ����ͼ�ۣ�
S=$\frac{1}{2}$FH•FM=$\frac{1}{2}$��2FM•FM=FM2=��AM+FN+BN-AB��2=��5t-10��2
=25t2-100t+100��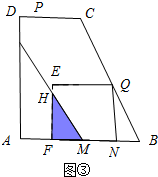
�ڵ�$\frac{5}{2}$��t��3ʱ����ͼ�ܣ�
EH=EQ-HQ=EQ-PC=EQ-��DC-DP��=6t-15��
FM=EH+BN=7t-15��
S=$\frac{1}{2}$��EH+FM��•EF=$\frac{1}{2}$��13t-30��•2t=13t2-30t��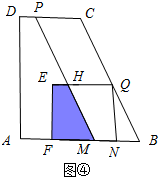
�۵�3��t��$\frac{10}{3}$ʱ����ͼ�ݢޣ�
S=S������EFNQ-S��HQI=��2t��2-$\frac{1}{2}$HQ•IQ
=4t2-��15-4t��2=-12t2+120t-225��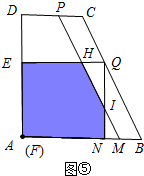
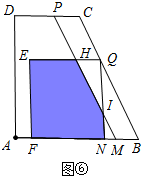
�ܵ�$\frac{10}{3}$��t��$\frac{15}{4}$ʱ����ͼ�ߣ�
S=S����ANQK-S��HQI=2t��10-t��-��15-4t��2=-18t2+140t-225��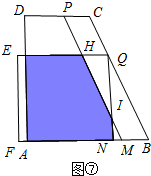
��4����ͼ�ۣ���HΪEF�е�ʱ������������
HF=t��FM=$\frac{1}{2}$t��MN=$\frac{3}{2}$t
2t+$\frac{3}{2}$t+t=10��t=$\frac{20}{9}$��
��ͼ�ܣ���ͼ�ο��Կ�����$\frac{5}{2}$��t��3ʱ������������
��ͼ�ޣ���I��QN���е�ʱ������������t=$\frac{10}{3}$��
���� ���⿼�������������ε����ʵ�Ӧ�ã�����Ĺؼ��Ǹ��ݲ�ͬ�����������Ӧ��ͼ�Σ�����ͼ�Σ����������ѧ��֪ʶ���г���ϵʽ��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
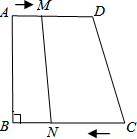 ��ͼ������ABCD�У�AD��CB����B=90�㣬AD=18cm��BC=21cm����M�ӵ�A��ʼ��AD��D����1cm/s���ٶ��ƶ�����N�ӵ�C��ʼ��CB�����B��2cm/s���ٶ��ƶ�����
��ͼ������ABCD�У�AD��CB����B=90�㣬AD=18cm��BC=21cm����M�ӵ�A��ʼ��AD��D����1cm/s���ٶ��ƶ�����N�ӵ�C��ʼ��CB�����B��2cm/s���ٶ��ƶ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
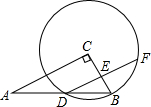 ��ͼ����Rt��ABC�У���C=90�㣬AB=10�����Ե�CΪԲ�ģ�CB��Ϊ�뾶��Բǡ�þ���AB���е�D����DF��AC����DF�ij�Ϊ5$\sqrt{3}$��
��ͼ����Rt��ABC�У���C=90�㣬AB=10�����Ե�CΪԲ�ģ�CB��Ϊ�뾶��Բǡ�þ���AB���е�D����DF��AC����DF�ij�Ϊ5$\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
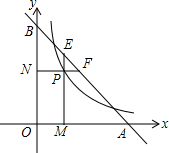 ��ͼ��ֱ��y=4-x��x�ᡢy����A��B���㣬P�Ƿ���������y=$\frac{2}{x}$��x��0��ͼ����λ��ֱ���·���һ�㣬����P��x��Ĵ��ߣ�����Ϊ��M����AB�ڵ�E������P��y��Ĵ��ߣ�����Ϊ��N����AB�ڵ�F����AF•BE=4��
��ͼ��ֱ��y=4-x��x�ᡢy����A��B���㣬P�Ƿ���������y=$\frac{2}{x}$��x��0��ͼ����λ��ֱ���·���һ�㣬����P��x��Ĵ��ߣ�����Ϊ��M����AB�ڵ�E������P��y��Ĵ��ߣ�����Ϊ��N����AB�ڵ�F����AF•BE=4���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com