
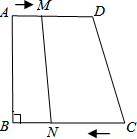
 如图,梯形ABCD中,AD∥CB,∠B=90°,AD=18cm,BC=21cm,点M从点A开始沿AD向D点以1cm/s的速度移动,点N从点C开始沿CB边向点B以2cm/s的速度移动,则:
如图,梯形ABCD中,AD∥CB,∠B=90°,AD=18cm,BC=21cm,点M从点A开始沿AD向D点以1cm/s的速度移动,点N从点C开始沿CB边向点B以2cm/s的速度移动,则:分析 (1)用t表示出MD、CN,然后根据平行四边形对边相等可得MD=CN,然后计算即可得解;
(2)表示出AM和BN的长,当AM=BN时四边形ABNM为矩形.
解答 解:(1)设t秒后四边形MNCD为平行四边形,
∵点M的速度为1cm/s,点N的速度为2cm/s,
∴MD=AD-AM=18-t,CN=2t,
四边形MNCD是平行四边形时,MD=CN,
∴18-t=2t,
解得t=6;
∴6秒时,四边形MNCD是平行四边形;
(2)根据题意得:AM=t,BN=21-2t,
当四边形ABNM为矩形时AM=BN,
即:t=21-2t,
解得:t=7,
∴7秒时,四边形ABNM为矩形.
点评 本题考查了梯形,平行四边形的性质,直角梯形的性质,等腰梯形的性质及矩形的判定,熟练掌握各图形的性质,分别列出关于t的方程是解题的关键.


科目:初中数学 来源: 题型:解答题
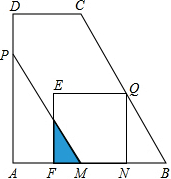 如图,在梯形ABCD中,AB∥CD,∠A=90°,AB=AD=10,CD=5,动点P从点A出发,沿折线AD-DC以每秒4个单位的速度向点C运动;点Q从点B出发,沿线段BC以每秒$\sqrt{5}$个单位的速度向点C运动,P,Q两点同时出发,当其中一点到达终点时,另一点也停止运动,过点P作PM∥BC交AB于M,过点Q作QN⊥AB交AB于N,以线段QN为一边在QN的左侧作正方形QEFN,设运动时间为t(s),线段PM扫过平面部分与正方形QEFN重叠部分的面积为S.
如图,在梯形ABCD中,AB∥CD,∠A=90°,AB=AD=10,CD=5,动点P从点A出发,沿折线AD-DC以每秒4个单位的速度向点C运动;点Q从点B出发,沿线段BC以每秒$\sqrt{5}$个单位的速度向点C运动,P,Q两点同时出发,当其中一点到达终点时,另一点也停止运动,过点P作PM∥BC交AB于M,过点Q作QN⊥AB交AB于N,以线段QN为一边在QN的左侧作正方形QEFN,设运动时间为t(s),线段PM扫过平面部分与正方形QEFN重叠部分的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 增减 | +20 | -30 | -25 | +15 | +30 |
| A. | 110 | B. | 120 | C. | 125 | D. | 130 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com