
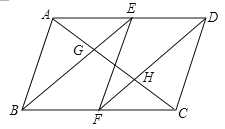
【题目】如图,在ABCD中,E、F分别为边AD、BC的中点,对角线AC分别交BE,DF于点G、H.求证:AG=CH.
【答案】证明见解析.
【解析】
试题分析:根据平行四边形的性质得到AD∥BC,得出∠ADF=∠CFH,∠EAG=∠FCH,证出四边形BFDE是平行四边形,得出BE∥DF,证出∠AEG=∠CFH,由ASA证明△AEG≌△CFH,得出对应边相等即可.
试题解析:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠ADF=∠CFH,∠EAG=∠FCH,∵E、F分别为AD、BC边的中点,∴AE=DE=![]() AD,CF=BF=
AD,CF=BF=![]() BC,∴DE∥BF,DE=BF,∴四边形BFDE是平行四边形,∴BE∥DF,∴∠AEG=∠ADF,∴∠AEG=∠CFH,在△AEG和△CFH中,∵∠EAG=∠FCH,AE=CF,∠AEG=∠CFH,∴△AEG≌△CFH(ASA),∴AG=CH.
BC,∴DE∥BF,DE=BF,∴四边形BFDE是平行四边形,∴BE∥DF,∴∠AEG=∠ADF,∴∠AEG=∠CFH,在△AEG和△CFH中,∵∠EAG=∠FCH,AE=CF,∠AEG=∠CFH,∴△AEG≌△CFH(ASA),∴AG=CH.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+bx+c中,函数y与自变量x的部分对应值如表:
x | … | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 10 | 5 | 2 | 1 | 2 | 5 | … |
若A(m,y1),B(m+6,y2)两点都在该函数的图象上,当m=时,y1=y2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设点(﹣1,y1),(2,y2),(3,y3)是抛物线y=﹣x2+a上的三点,则y1、y2、y3的大小关系为( )
A.y3>y2>y1B.y1>y3>y2C.y3>y1>y2D.y1>y2>y3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】哈市某花卉种植基地欲购进甲、乙两种君子兰进行培育,若购进甲种2株,乙种3株,则共需要成本1700元;若购进甲种3株,乙种1株,则共需要成本1500元.
(1)求甲乙两种君子兰每株成本分别为多少元?
(2)该种植基地决定在成本不超过30000元的前提下购进甲、乙两种君子兰,若购进乙种君子兰的株数比甲种君子兰的3倍还多10株,求最多购进甲种君子兰多少株?
查看答案和解析>>
科目:初中数学 来源: 题型:
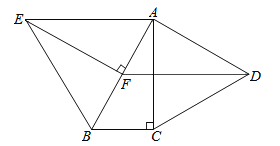
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知:∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某兴趣小组开展课外活动.如图,A,B两地相距12米,小明从点A出发沿AB方向匀速前进,2秒后到达点D,此时他(CD)在某一灯光下的影长为AD,继续按原速行走2秒到达点F,此时他在同一灯光下的影子仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H,此时他(GH)在同一灯光下的影长为BH(点C,E,G在一条直线上).
(1)请在图中画出光源O点的位置,并画出他位于点F时在这个灯光下的影长FM(不写画法);
(2)求小明原来的速度.
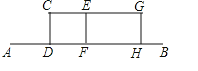
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com