
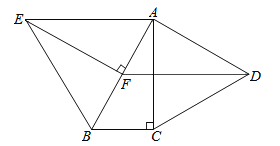
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知:∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)首先由Rt△ABC中,由∠BAC=30°可以得到AB=2BC,又由△ABE是等边三角形,EF⊥AB,由此得到AE=2AF,并且AB=2AF,然后证得△AFE≌△BCA,继而证得结论;
(2)根据(1)知道EF=AC,而△ACD是等边三角形,所以EF=AC=AD,并且AD⊥AB,而EF⊥AB,由此得到EF∥AD,再根据平行四边形的判定定理即可证明四边形ADFE是平行四边形.
试题解析:(1)∵Rt△ABC中,∠BAC=30°,∴AB=2BC,又∵△ABE是等边三角形,EF⊥AB,∴AB=2AF
∴AF=BC,在Rt△AFE和Rt△BCA中,∵AF=BC,AE=BA,∴Rt△AFE≌Rt△BCA(HL),∴AC=EF;
(2)∵△ACD是等边三角形,∴∠DAC=60°,AC=AD,∴∠DAB=∠DAC+∠BAC=90°
又∵EF⊥AB,∴EF∥AD,∵AC=EF,AC=AD,∴EF=AD,∴四边形ADFE是平行四边形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某车队要把4000吨货物运到雅安地震灾区(方案定后,每天的运量不变)。
(1)从运输开始,每天运输的货物吨数n(单位:吨)与运输时间t(单位:天)之间有怎样的函数关系式?
(2)因地震,到灾区的道路受阻,实际每天比原计划少运20%,则推迟1天完成任务,求原计划完成任务的天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,BO平分∠ABC,CO平分∠ACB,MN过点O,交AB于M,交AC于N,且MN∥BC,若AB=12cm,AC=18cm,则△AMN周长为 . 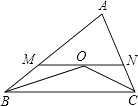
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Pn表示n边形的对角线的交点个数(指落在其内部的交点),如果这些交点都不重合,那么Pn与n的关系式是:Pn=![]() (其中a,b是常数,n≥4)
(其中a,b是常数,n≥4)
(1)通过画图,可得:四边形时,P4= ;五边形时,P5= ;
(2)请根据四边形和五边形对角线交点的个数,结合关系式,求a,b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四川汶川地震灾后重建中,某公司拟为灾区援建一所希望学校.公司经过调查了解:甲、乙两个工程队有能力承包建校工程,甲工程队单独完成建校工程的时间是乙工程队的1.5倍,甲、乙两队合作完成建校工程需要72天.
(1)甲、乙两队单独完成建校工程各需多少天?
(2)在施工过程中,该公司派一名技术人员在现场对施工质量进行全程监督,每天需要补助100元.若由甲工程队单独施工时平均每天的费用为0.8万元.现公司选择了乙工程队,要求其施工总费用不能超过甲工程队,则乙工程队单独施工时平均每天的费用最多为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com