
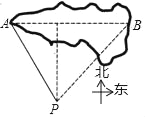
【题目】在数学活动课上,九年级(1)班数学兴趣小组的同学们要测量某公园人工湖亭子A与它正东方向的亭子B之间的距离,现测得亭子A位于点P北偏西30°方向,亭子B位于点P北偏东42°方向,测得点P与亭子A之间的距离为200米,求亭子A与亭子B之间的距离.(结果精确到1米)
【参考数据:sin42°=0.67,cos42°=0.74,tan42°=0.90, ![]() =1.73】
=1.73】
科目:初中数学 来源: 题型:
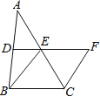
【题目】图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到F,使得EF=BE,连接CF.
(1)求证:四边形BCFE是菱形.
(2)若DE=4cm,∠EBC=60°,求菱形BCFE的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三个有理数x,y,z,若x=![]() ,且x与y互为相反数,y是z的倒数.
,且x与y互为相反数,y是z的倒数.
(1)当n为奇数时,你能求出x,y,z这三个数吗?当n为偶数时,你能求出x,y,z,这三个数吗?若能,请计算并写出结果;若不能,请说明理由.
(2)根据(1)的结果计算:xy﹣yn﹣(y﹣z)2019的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
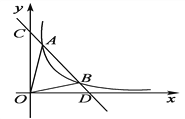
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x>0)的图象交于A(m,6),B(3,n)两点.
(x>0)的图象交于A(m,6),B(3,n)两点.
(1)求一次函数的解析式;
(2)根据图象直接写出kx+b-![]() <0时x的取值范围;
<0时x的取值范围;
(3)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列方程变形中,正确的是( )
A.方程3x-2=2x+1,移项,得3x-2x=1-2
B.方程3-x=2-5(x-1),去括号,得3-x=2-5x-1;
C.方程-75x=76,方程两边同除以-75,得x=-![]()
D.方程![]() =1+
=1+![]() ,去分母,得2(2x-1)=6+3(x-3)
,去分母,得2(2x-1)=6+3(x-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
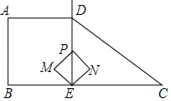
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,射线ED⊥BC于点E,AD=AB=BE=![]() BC=4,动点P从点E出发,沿射线ED以每秒2个单位长度的速度运动,以PE为对角线做正方形PMEN,设运动时间为t秒,正方形PMEN与四边形ABCD重叠部分面积为S.
BC=4,动点P从点E出发,沿射线ED以每秒2个单位长度的速度运动,以PE为对角线做正方形PMEN,设运动时间为t秒,正方形PMEN与四边形ABCD重叠部分面积为S.
(1)当点N落在边DC上时,求t的值.
(2)求S与t的函数关系式.
(3)当正方形PMEN被直线BD分成2:1两部分时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形 ABCD 的边长为 1,以顶点 A、B 为圆心,1 为半径的两弧交于点 E, 以顶点 C、D 为圆心,1 为半径的两弧交于点 F,则 EF 的长为 ( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为民中学租用两辆速度相同的小汽车送1名带队老师和6名学生到城区中学参加数学竞赛,每辆限坐4人(不包括司机).其中一辆小汽车在距离考场16.5 km的地方出现故障,此时离截止进考场的时刻还有50分钟,这时唯一可利用的交通工具是另一辆小汽车,且这辆车的平均速度是55 km/h,人步行的速度是5 km/h(上、下车时间忽略不计).
(1)若小汽车送4人到达考场,然后再回到出故障处接其他人,请你通过计算说明他们能否在截止进考场的时刻前到达考场;
(2)假如你是带队的老师,请设计一种你认为较优的运送方案,使他们能在截止进考场的时刻前到达考场,并通过计算说明方案的可行性.
查看答案和解析>>
科目:初中数学 来源: 题型:
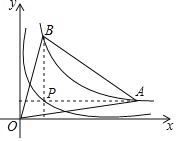
【题目】如图,点P为函数y=![]() (x>0)图象上一点过点P作x轴、y轴的平行线,分别与函数y
(x>0)图象上一点过点P作x轴、y轴的平行线,分别与函数y![]() (x>0)的图象交于点A,B,则△AOB的面积为_____.
(x>0)的图象交于点A,B,则△AOB的面积为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com