
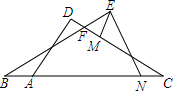
 已知,如图,∠EBN+∠FCA=∠MEN,AB=CN,EN=AD.EM∥AD.探究BF与CF之间的数量关系.
已知,如图,∠EBN+∠FCA=∠MEN,AB=CN,EN=AD.EM∥AD.探究BF与CF之间的数量关系. 分析 过点A作AG⊥CD于点G,过N作NH⊥BE于点H,首先证明△ADG≌△NEH证得AG=NH,然后证明△ACG≌△NBH,证明∠B=∠C,然后利用等角对等边证明.
解答 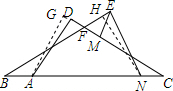 解:过点A作AG⊥CD于点G,过N作NH⊥BE于点H.
解:过点A作AG⊥CD于点G,过N作NH⊥BE于点H.
∵∠MEN-∠B+∠C=∠MFE,
∴∠NEH=∠MEN+∠FEM=∠MFE+∠FEM=∠CME.
∵ME∥AD,
∴∠ADF=∠FME,
∴∠ADG=∠CME=∠NEH.
在△ADG和△NEH中,
$\left\{\begin{array}{l}{∠ADG=∠NEH}\\{∠G=∠NHE}\\{AD=NE}\end{array}\right.$,
∴△ADG≌△NEH,
∴AG=NH.
∵AB=CN,
∴AC=NB,
在直角△ACG和直角△NBH中,
$\left\{\begin{array}{l}{AC=NB}\\{AG=NH}\end{array}\right.$,
∴直角△ACG≌直角△NBH,
∴∠C=∠B,
∴BF=CF.
点评 本题考查了全等三角形的判定与性质,正确作出辅助线,证明∠ADG=∠NEH是本题的关键.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
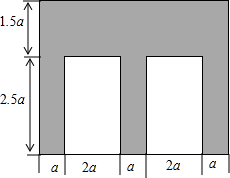 某公园一块草坪的形状如图所示(阴影部分).
某公园一块草坪的形状如图所示(阴影部分).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com