
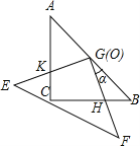
°ĺŐ‚ńŅ°Ņį—ŃĹłŲ»ęĶ»ĶńĶ»—Ł÷ĪĹ«»żĹ«įŚABCļÕEFGĶĢ∑Ň‘ŕ“Ľ∆ū£¨«“ Ļ»żĹ«įŚEFGĶń÷ĪĹ«∂•Ķ„G”Ž»żĹ«įŚABCĶń–ĪĪŖ÷–Ķ„O÷ōļŌ£ģŌ÷Ĺ껿ūįŚEFG»∆OĶ„ň≥ Ī’Ž∑ĹŌÚ–ż◊™£®–ż◊™Ĺ«¶Ń¬ķ◊„ŐűľĢ£ļ0°„£ľ¶Ń£ľ90°„£©£¨ňńĪŖ–őCHGK «–ż◊™Ļż≥Ő÷–ŃĹ»żĹ«įŚĶń÷ōĶĢ≤Ņ∑÷£¨“—÷™AC=4£ģ‘ŕ–ż◊™Ļż≥Ő÷–£¨Ō¬Ń–ĹŠ¬Ř£ļĘŔBH=CK£ĽĘŕňńĪŖ–őCHGKĶń√śĽżĶ»”ŕ4£ĽĘŘGK≥§∂»Ķń◊Óīů÷Ķő™2![]() £ĽĘ‹ŌŖ∂őKHĶń≥§∂»◊Ó–°÷Ķő™2
£ĽĘ‹ŌŖ∂őKHĶń≥§∂»◊Ó–°÷Ķő™2![]() £ģ∆š÷–’ż»∑Ķń”–£®°°°°£©łŲ
£ģ∆š÷–’ż»∑Ķń”–£®°°°°£©łŲ
A.1B.2C.3D.4
°ĺīūįł°ŅD
°ĺĹ‚őŲ°Ņ
”…Ķ»—Ł÷ĪĹ«»żĹ«–őĶń–‘÷ Ņ…Ň–∂ŌĘŘ£¨°ĪASA°įŅ…÷§°ųBGH°’°ųCGK£¨Ņ…Ķ√CK=BH£¨S°ųCKG=S°ųBHG£¨Ņ…Ň–∂ŌĘŔĘŕ£¨”…ĻīĻ…∂®ņŪļÕ∂ĢīőļĮ ż–‘÷ Ņ…Ň–∂ŌĘ‹£ģ
Ĺ‚£ļѨŔCG£¨
°ŖAC=BC=4£¨°ŌACB=90°„£¨G «AB÷–Ķ„£¨
°ŗ°ŌACG=°ŌB=45°„£¨AB=4![]() £¨CG=BG=2
£¨CG=BG=2![]() £¨CG°ÕAB£¨
£¨CG°ÕAB£¨
°ŗĶĪĶ„K”ŽĶ„C÷ōļŌ Ī£¨GK”–◊Óīů÷Ķő™2![]() £¨
£¨
Ļ ĘŘ’ż»∑£¨
°Ŗ°ŌKGH=°ŌCGB=90°„£¨
°ŗ°ŌKGC=°ŌBGH£¨«“CG=BG£¨°ŌB=°ŌGCA£¨
°ŗ°ųBGH°’°ųCGK£®ASA£©£¨
°ŗCK=BH£¨S°ųCKG=S°ųBHG£¨
°ŗSňńĪŖ–őCKGH=S°ųBGC=![]() S°ųBCA=4£¨
S°ųBCA=4£¨
Ļ ĘŔĘŕ’ż»∑£¨
°ŖBH=CK
°ŗCH=4-CK
°ŖKH2=£®4-CK£©2+CK2=2£®CK-2£©2+8
°ŗĶĪCK=2 Ī£¨KH”–◊Ó–°÷Ķ2![]()
Ļ Ę‹’ż»∑
Ļ —°£ļD£ģ


 Ņžņ÷ ÓľŔ ÓľŔń‹Ń¶◊‘≤‚÷–őų ťĺ÷ŌĶŃ–īūįł
Ņžņ÷ ÓľŔ ÓľŔń‹Ń¶◊‘≤‚÷–őų ťĺ÷ŌĶŃ–īūįł
| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ≥ň∑®Ļę ĹĶńŐĹĺŅľį”¶”√£ģ
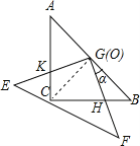
ż—߼Ó∂ĮŅő…Ō£¨ņŌ ¶◊ľĪłŃň»Űł…łŲ»ÁÕľ1Ķń»ż÷÷÷Ĺ∆¨£¨![]() ÷÷÷Ĺ∆¨ĪŖ≥§ő™
÷÷÷Ĺ∆¨ĪŖ≥§ő™![]() Ķń’ż∑Ĺ–ő£¨
Ķń’ż∑Ĺ–ő£¨![]() ÷÷÷Ĺ∆¨ «ĪŖ≥§ő™
÷÷÷Ĺ∆¨ «ĪŖ≥§ő™![]() Ķń’ż∑Ĺ–ő£¨
Ķń’ż∑Ĺ–ő£¨![]() ÷÷÷Ĺ∆¨≥§ő™
÷÷÷Ĺ∆¨≥§ő™![]() °ĘŅŪő™
°ĘŅŪő™![]() Ķń≥§∑Ĺ–ő£¨≤Ę”√
Ķń≥§∑Ĺ–ő£¨≤Ę”√![]() ÷÷÷Ĺ∆¨“Ľ’Ň£¨
÷÷÷Ĺ∆¨“Ľ’Ň£¨![]() ÷÷÷Ĺ∆¨“Ľ’Ň£¨
÷÷÷Ĺ∆¨“Ľ’Ň£¨![]() ÷÷÷Ĺ∆¨ŃĹ’Ň∆ī≥…»ÁÕľ2Ķńīů’ż∑Ĺ–ő£ģ
÷÷÷Ĺ∆¨ŃĹ’Ň∆ī≥…»ÁÕľ2Ķńīů’ż∑Ĺ–ő£ģ
£®1£©ĻŘ≤žÕľ2£¨«Žń„–ī≥ŲŌ¬Ń–»żłŲīķ ż Ĺ£ļ![]() £¨
£¨![]() £¨
£¨![]() ÷ģľšĶńĶ»ŃŅĻōŌĶ£ģ£Ľ
÷ģľšĶńĶ»ŃŅĻōŌĶ£ģ£Ľ
£®2£©»Ű“™∆ī≥Ų“ĽłŲ√śĽżő™![]() Ķńĺō–ő£¨‘Ú–Ť“™
Ķńĺō–ő£¨‘Ú–Ť“™![]() ļŇŅ®∆¨1’Ň£¨
ļŇŅ®∆¨1’Ň£¨![]() ļŇŅ®∆¨2’Ň£¨
ļŇŅ®∆¨2’Ň£¨![]() ļŇŅ®∆¨ ’Ň£ģ
ļŇŅ®∆¨ ’Ň£ģ
£®3£©łýĺ›£®1£©Ő‚÷–ĶńĶ»ŃŅĻōŌĶ£¨Ĺ‚ĺŲ»ÁŌ¬ő Ő‚£ļ
ĘŔ“—÷™£ļ![]() £¨
£¨![]() £¨«ů
£¨«ů![]() Ķń÷Ķ£Ľ
Ķń÷Ķ£Ľ
Ęŕ“—÷™![]() £¨«ů
£¨«ů![]() Ķń÷Ķ£ģ
Ķń÷Ķ£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ‘ŕňģĻŻŌķ ŘÕķľĺ£¨ń≥ňģĻŻĶÍĻļĹÝ“Ľ”Ň÷ ňģĻŻ£¨ĹÝľŘő™20‘™/«ßŅň£¨ ŘľŘ≤ĽĶÕ”ŕ20‘™/«ßŅň£¨«“≤Ľ≥¨Ļż32‘™/«ßŅň£¨łýĺ›Ōķ Ř«ťŅŲ£¨∑ĘŌ÷ł√ňģĻŻ“ĽŐžĶńŌķ ŘŃŅy£®«ßŅň£©”Žł√ŐžĶń ŘľŘx£®‘™/«ßŅň£©¬ķ◊„»ÁŌ¬ĪŪňý ĺĶń“ĽīőļĮ żĻōŌĶ£ģ
Ōķ ŘŃŅy£®«ßŅň£© | °≠ | 34.8 | 32 | 29.6 | 28 | °≠ |
ŘľŘx£®‘™/«ßŅň£© | °≠ | 22.6 | 24 | 25.2 | 26 | °≠ |
£®1£©ń≥Őž’‚÷÷ňģĻŻĶń ŘľŘő™23.5‘™/«ßŅň£¨«ůĶĪŐžł√ňģĻŻĶńŌķ ŘŃŅ£ģ
£®2£©»ÁĻŻń≥ŐžŌķ Ř’‚÷÷ňģĻŻĽŮņŻ150‘™£¨ń«√īł√ŐžňģĻŻĶń ŘľŘő™∂ŗ…Ŕ‘™£Ņ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
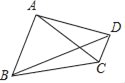
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕňńĪŖ–őABCD÷–£¨AC°ĘBD «∂‘Ĺ«ŌŖ£¨AC=AD£¨BC£ĺAB£¨AB°őCD£¨AB=4£¨BD=2![]() £¨tan°ŌBAC=3
£¨tan°ŌBAC=3![]() £¨‘ÚŌŖ∂őBCĶń≥§ «_____£ģ
£¨‘ÚŌŖ∂őBCĶń≥§ «_____£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»Űį—≤ĽĶ» Ĺ◊ť![]() ĶńĹ‚ľĮ‘ŕ ż÷Š…ŌĪŪ ĺ≥Ųņī£¨‘Ú∆š∂‘”¶ĶńÕľ–őő™
ĶńĹ‚ľĮ‘ŕ ż÷Š…ŌĪŪ ĺ≥Ųņī£¨‘Ú∆š∂‘”¶ĶńÕľ–őő™
A. ≥§∑Ĺ–ő B. ŌŖ∂ő C. …šŌŖ D. ÷ĪŌŖ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
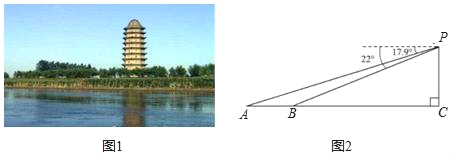
°ĺŐ‚ńŅ°Ņň ŃĘ‘ŕŃŔ«Ś –≥«ĪĪīů‘ňļ”∂ęį∂Ķń…ŠņŻĪ¶ňĢ£¨ «°į‘ňļ”ňńīů√ŻňĢ°Ī÷ģ“Ľ£®»ÁÕľ1£©. ż—ß–ň»§–°◊ťĶń–°ŃŃÕ¨—ß‘ŕňĢ…ŌĻŘĺįĶ„Pī¶£¨ņŻ”√≤‚Ĺ«“«≤‚Ķ√‘ňļ”ŃĹį∂…ŌĶńA£¨BŃĹĶ„Ķńł©Ĺ«∑÷Īūő™17.9°„£¨22°„£¨≤Ę≤‚Ķ√ňĢĶ◊Ķ„CĶĹĶ„BĶńĺŗņŽő™142√◊£®A°ĘB°ĘC‘ŕÕ¨“Ľ÷ĪŌŖ…Ō£¨»ÁÕľ2£©£¨«ů‘ňļ”ŃĹį∂…ŌĶńA°ĘBŃĹĶ„ĶńĺŗņŽ£®ĺę»∑ĶĹ1√◊£©.£®≤őŅľ żĺ›£ļsin22°„°÷0.37£¨cos22°„°÷0.93£¨tan22°„°÷0.40£¨sin17.9°„°÷0.31£¨cos17.9°„°÷0.95£¨tan17.9°„°÷0.32£©
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
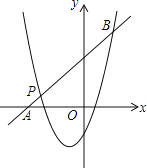
°ĺŐ‚ńŅ°Ņ“—÷™∂ĢīőļĮ ży1=x2+mx+nĶńÕľŌůĺ≠ĻżĶ„P£®©Ā3£¨1£©£¨∂‘≥∆÷Š «ĺ≠Ļż£®©Ā1£¨0£©«“∆Ĺ––”ŕy÷ŠĶń÷ĪŌŖ£ģ
£®1£©«ům£¨nĶń÷Ķ£ģ
£®2£©»ÁÕľ£¨“ĽīőļĮ ży2=kx+bĶńÕľŌůĺ≠ĻżĶ„P£¨”Žx÷ŠŌŗĹĽ”ŕĶ„A£¨”Ž∂ĢīőļĮ żĶńÕľŌůŌŗĹĽ”ŕŃŪ“ĽĶ„B£¨Ķ„B‘ŕĶ„PĶń”“≤ŗ£¨PA£ļPB=1£ļ5£¨«ů“ĽīőļĮ żĶńĪŪīÔ Ĺ£ģ
£®3£©÷ĪĹ”–ī≥Ųy1£ĺy2 ĪxĶń»°÷Ķ∑∂őߣģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™£¨‘ŕ°ųABC÷–£¨°ŌBAC=90°„£¨°ŌABC=45°„£¨Ķ„Dő™÷ĪŌŖBC…Ō“Ľ∂ĮĶ„£®Ķ„D≤Ľ”ŽĶ„B£¨C÷ōļŌ£©£ģ“‘ADő™ĪŖ◊Ų’ż∑Ĺ–őADEF£¨Ń¨Ĺ”CF

£®1£©»ÁÕľ1£¨ĶĪĶ„D‘ŕŌŖ∂őBC…Ō Ī£ģ«ů÷§CF+CD=BC£Ľ
£®2£©»ÁÕľ2£¨ĶĪĶ„D‘ŕŌŖ∂őBCĶń—”≥§ŌŖ…Ō Ī£¨∆šňŻŐűľĢ≤ĽĪš£¨«Ž÷ĪĹ”–ī≥ŲCF£¨BC£¨CD»żŐűŌŖ∂ő÷ģľšĶńĻōŌĶ£Ľ
£®3£©»ÁÕľ3£¨ĶĪĶ„D‘ŕŌŖ∂őBCĶń∑īŌÚ—”≥§ŌŖ…Ō Ī£¨«“Ķ„A£¨F∑÷Īū‘ŕ÷ĪŌŖBCĶńŃĹ≤ŗ£¨∆šňŻŐűľĢ≤ĽĪš£Ľ
ĘŔ«Ž÷ĪĹ”–ī≥ŲCF£¨BC£¨CD»żŐűŌŖ∂ő÷ģľšĶńĻōŌĶ£Ľ
Ęŕ»Ű’ż∑Ĺ–őADEFĶńĪŖ≥§ő™![]() £¨∂‘Ĺ«ŌŖAE£¨DFŌŗĹĽ”ŕĶ„O£¨Ń¨Ĺ”OC£ģ«ůOCĶń≥§∂»£ģ
£¨∂‘Ĺ«ŌŖAE£¨DFŌŗĹĽ”ŕĶ„O£¨Ń¨Ĺ”OC£ģ«ůOCĶń≥§∂»£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
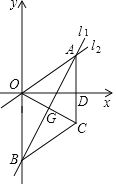
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ÷–£¨÷ĪŌŖl£ļy![]() x”Ž÷ĪŌŖl£ļy=kx+bŌŗĹĽ”ŕĶ„A£®a£¨3£©£¨÷ĪŌŖĹĽlĹĽy÷Š”ŕĶ„B£®0£¨©Ā5£©£ģ
x”Ž÷ĪŌŖl£ļy=kx+bŌŗĹĽ”ŕĶ„A£®a£¨3£©£¨÷ĪŌŖĹĽlĹĽy÷Š”ŕĶ„B£®0£¨©Ā5£©£ģ
£®1£©«ů÷ĪŌŖlĶńĹ‚őŲ Ĺ£Ľ
£®2£©Ĺę°ųOAB—ō÷ĪŌŖl∑≠’ŘĶ√ĶĹ°ųCAB£®∆š÷–Ķ„OĶń∂‘”¶Ķ„ő™Ķ„C£©£¨«ů÷§£ļAC°őOB£Ľ
£®3£©‘ŕ÷ĪŌŖBCŌ¬∑Ĺ“‘BCő™ĪŖ◊ųĶ»—Ł÷ĪĹ«»żĹ«–őBCP£¨÷ĪĹ”–ī≥ŲĶ„PĶń◊ÝĪÍ£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ļķľ —ß–£”Ň—° - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com