
【题目】已知点![]() ,
,![]() 在二次函数
在二次函数![]() 的图象上,点
的图象上,点![]() 是函数图象的顶点,则( )
是函数图象的顶点,则( )
A.当![]() 时,
时,![]() 的取值范围是
的取值范围是![]()
B.当![]() 时,
时,![]() 的取值范围是
的取值范围是![]()
C.当![]() 时,
时,![]() 的取值范围是
的取值范围是![]()
D.当![]() 时,
时,![]() 的取值范围是
的取值范围是![]()
【答案】B
【解析】
由![]() 判断出函数有最大值,开口向下,然后根据两点
判断出函数有最大值,开口向下,然后根据两点![]() ,
,![]() 在对称同侧和异侧两种情况分类讨论,利用抛物线的对称轴的位置确定x0的取值范围;由
在对称同侧和异侧两种情况分类讨论,利用抛物线的对称轴的位置确定x0的取值范围;由![]() 判断出函数有最小值,开口向上,然后根据两点
判断出函数有最小值,开口向上,然后根据两点![]() ,
,![]() 在对称轴同侧和异侧两种情况分类讨论,利用抛物线的对称轴的位置确定x0的取值范围.
在对称轴同侧和异侧两种情况分类讨论,利用抛物线的对称轴的位置确定x0的取值范围.
解:设抛物线的对称轴为直线x=-![]() ,即顶点横坐标x0=-
,即顶点横坐标x0=-![]() ,
,
A,B选项中,由![]() 可知函数有最大值,图象开口向下,①当
可知函数有最大值,图象开口向下,①当![]() ,
,![]() 在对称轴同侧时,若
在对称轴同侧时,若![]() 成立,则有抛物线的对称轴-
成立,则有抛物线的对称轴-![]() ≤-3,∴x0≤-3;②当
≤-3,∴x0≤-3;②当![]() ,
,![]() 在对称轴的异侧时,若
在对称轴的异侧时,若![]() 成立,可得抛物线的对称轴-3<-
成立,可得抛物线的对称轴-3<-![]() <
<![]() =1,此时-3<x0<1,综合①②可得x0的取值范围为x0<1.故A错误,B正确;
=1,此时-3<x0<1,综合①②可得x0的取值范围为x0<1.故A错误,B正确;
C,D选项中,由![]() 可知函数有最小值,图象开口向上,①当
可知函数有最小值,图象开口向上,①当![]() ,
,![]() 在对称轴同侧时,若
在对称轴同侧时,若![]() 成立,则有抛物线的对称轴-
成立,则有抛物线的对称轴-![]() ≥5,∴x0≥5;②当
≥5,∴x0≥5;②当![]() ,
,![]() 在对称轴的异侧时,若
在对称轴的异侧时,若![]() 成立,可得抛物线的对称轴1<-
成立,可得抛物线的对称轴1<-![]() <5,此时1<x0<5,综合①②可得x0的取值范围为x0>1.故C错误,D错误.
<5,此时1<x0<5,综合①②可得x0的取值范围为x0>1.故C错误,D错误.
故选:B.


科目:初中数学 来源: 题型:
【题目】问题提出
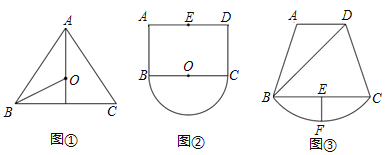
(1)如图①,在△ABC中,AB=AC=10,BC=12,点O是△ABC的外接圆的圆心,则OB的长为
问题探究
(2)如图②,已知矩形ABCD,AB=4,AD=6,点E为AD的中点,以BC为直径作半圆O,点P为半圆O上一动点,求E、P之间的最大距离;
问题解决
(3)某地有一块如图③所示的果园,果园是由四边形ABCD和弦CB与其所对的劣弧场地组成的,果园主人现要从入口D到![]() 上的一点P修建一条笔直的小路DP.已知AD∥BC,∠ADB=45°,BD=120
上的一点P修建一条笔直的小路DP.已知AD∥BC,∠ADB=45°,BD=120![]() 米,BC=160米,过弦BC的中点E作EF⊥BC交
米,BC=160米,过弦BC的中点E作EF⊥BC交![]() 于点F,又测得EF=40米.修建小路平均每米需要40元(小路宽度不计),不考虑其他因素,请你根据以上信息,帮助果园主人计算修建这条小路最多要花费多少元?
于点F,又测得EF=40米.修建小路平均每米需要40元(小路宽度不计),不考虑其他因素,请你根据以上信息,帮助果园主人计算修建这条小路最多要花费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
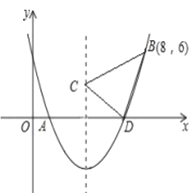
【题目】如图,二次函数![]() 的图象交
的图象交![]() 轴于
轴于![]() 两点,并经过
两点,并经过![]() 点,已知
点,已知![]() 点坐标是
点坐标是![]() ,
,![]() 点坐标是
点坐标是![]() .
.
(1)求二次函数的解析式;
(2)求函数图象的顶点坐标及![]() 点的坐标;
点的坐标;
(3)二次函数的对称轴上是否存在一点![]() ,使得
,使得![]() 的周长最小?若
的周长最小?若![]() 点存在,求出
点存在,求出![]() 点的坐标,若
点的坐标,若![]() 点不存在,请说明理由.
点不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
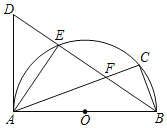
【题目】如图,以AB为直径作半圆O,点C是半圆上一点,∠ABC的平分线交⊙O于E,D为BE延长线上一点,且DE=FE.
(1)求证:AD为⊙O切线;
(2)若AB=20,tan∠EBA=![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划购买2台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元,三年后如果备件多余,每个以![]() 元(
元(![]() )回收.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得到如下频数分布直方图:
)回收.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得到如下频数分布直方图:
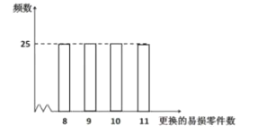
记![]() 表示2台机器三年内共需更换的易损零件数,
表示2台机器三年内共需更换的易损零件数,![]() 表示购买2台机器的同时购买的易损零件数.
表示购买2台机器的同时购买的易损零件数.
(1)以100台机器为样本,请利用画树状图或列表的方法估计![]() 不超过19的概率;
不超过19的概率;
(2)以这100台机器在购买易损零件上所需费用的平均数为决策依据,在![]() 与
与![]() 之中选其一,当
之中选其一,当![]() 为何值时,选
为何值时,选![]() 比较划算?
比较划算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,自左至右,第1个图由1个正六边形、6个正方形和6个等边三角形组成;第2个图由2个正六边形、11个正方形和10个等边三角形组成;第3个图由3个正六边形、16个正方形和14个等边三角形组成;…按照此规律,第![]() 个图中正方形和等边三角形的个数之和为 个.
个图中正方形和等边三角形的个数之和为 个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“过直线外一点作这条直线的平行线”的尺规作图过程.
已知:如图1,直线BC及直线BC外一点P.
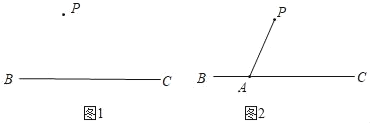
求作:直线PE,使得PE∥BC.
作法:如图2.
①在直线BC上取一点A,连接PA;
②作∠PAC的平分线AD;
③以点P为圆心,PA长为半径画弧,交射线AD于点E;
④作直线PE.
所以直线PE就是所求作的直线.根据小明设计的尺规作图过程.
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:∵AD平分∠PAC,
∴∠PAD=∠CAD.
∵PA=PE,
∴∠PAD= ,
∴∠PEA= ,
∴PE∥BC.( )(填推理依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,函数![]() (x>0)的图象与直线l1:
(x>0)的图象与直线l1:![]() 交于点A,与直线l2:x=k交于点B.直线l1与l2交于点C.
交于点A,与直线l2:x=k交于点B.直线l1与l2交于点C.

(1) 当点A的横坐标为1时,则此时k的值为 _______;
(2) 横、纵坐标都是整数的点叫做整点. 记函数![]() (x>0) 的图像在点A、B之间的部分与线段AC,BC围成的区域(不含边界)为W.
(x>0) 的图像在点A、B之间的部分与线段AC,BC围成的区域(不含边界)为W.
①当k=3时,结合函数图像,则区域W内的整点个数是_________;
②若区域W内恰有1个整点,结合函数图象,直接写出k的取值范围:___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com