
【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格图中进行下列操作:
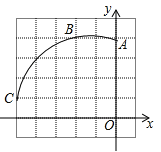
(1)利用网格确定该圆弧所在圆的圆心D点的位置,并写出点D坐标为 ;
(2)连接AD、CD,则⊙D的半径为 (结果保留根号),∠ADC的度数为 ;
(3)若扇形DAC是一个圆锥的侧面展开图,则该圆锥底面半径为 .(结果保留根号).
【答案】(1)作图见解析,(-1,0);(2)![]() ,90°;(3)
,90°;(3)![]() .
.
【解析】
试题分析:(1)根据线段垂直平分线性质找出D即可;
(2)根据勾股定理即可求出CD,证△CED≌△DOA,根据全等三角形的性质求出∠COE=∠OAD,根据三角形内角和定理即可求出∠ADC;
(3)根据弧长公式求出弧长,根据圆的周长公式求出即可.
试题解析:(1)如图:
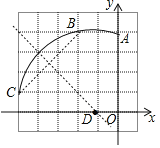
D的坐标为(-1,0).
(2)如图:
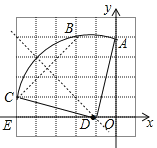
设小正方形的边长为1,由勾股定理得:CD=![]() ,
,
在△CED和△DOA中
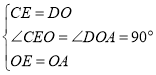
∴△CED≌△DOA,
∴∠COE=∠OAD,
∵∠AOD=90°,
∴∠OAD+∠ADO=90°,
∴∠ADC=180°-(∠CDE+∠ADO)=180°-(∠OAD+∠ADO)=180°-90°=90°
(3)![]() 的长为
的长为![]() ,
,
设圆锥底面半径为r,
则2πr=![]() ,
,
解得:r=![]() .
.


科目:初中数学 来源: 题型:
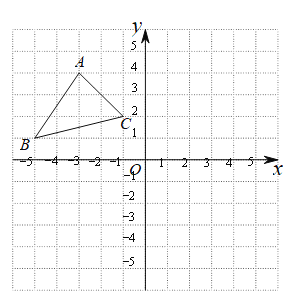
【题目】如图,在平面直角坐标系xOy中,△ABC的三个顶点分别为A(-3,4),B(-5,1),C(-1,2).
(1)画出△ABC关于原点对称的△A1B1C1,并写出点B1的坐标;
(2)画出△ABC绕原点逆时针旋转90°后的△A2B2C2,并写出点B2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
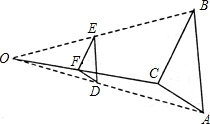
【题目】按如下方法,将△ABC的三边缩小的原来的![]() ,如图,任取一点O,连AO、BO、CO,并取它们的中点D、E、F,得△DEF,则下列说法正确的个数是( )
,如图,任取一点O,连AO、BO、CO,并取它们的中点D、E、F,得△DEF,则下列说法正确的个数是( )
①△ABC与△DEF是位似图形②△ABC与△DEF是相似图形
③△ABC与△DEF的周长比为1:2④△ABC与△DEF的面积比为4:1.
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.

(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新华商场为迎接家电下乡活动销售某种冰箱,每台进价为2500元,市场调研表明;当销售价定为2900元时,平均每天能售出8台;而当销售价每降低50元时,平均每天就能多售出4台,商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:平面内点A到图形G上各个点的距离的最小值称为该点到这个图形的最小距离d,点A到图形G上各个点的距离的最大值称为该点到这个图形的最大距离D,定义点A到图形G的距离跨度为R=D-d.
(1)①如图1,在平面直角坐标系xOy中,图形G1为以O为圆心,2为半径的圆,直接写出以下各点到图形G1的距离跨度:
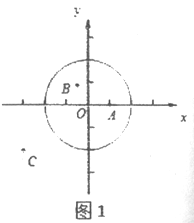
A(1,0)的距离跨度______________;
B(-![]() ,
, ![]() )的距离跨度____________;
)的距离跨度____________;
C(-3,-2)的距离跨度____________;
②根据①中的结果,猜想到图形G1的距离跨度为2的所有的点组成的图形的形状是______________.
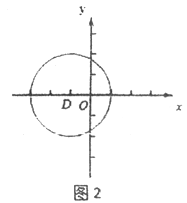
(2)如图2,在平面直角坐标系xOy中,图形G2为以D(-1,0)为圆心,2为半径的圆,直线y=k(x-1)上存在到G2的距离跨度为2的点,求k的取值范围.
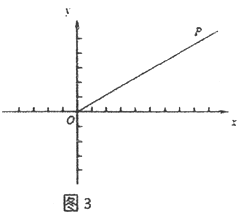
(3)如图3,在平面直角坐标系xOy中,射线OP:y=![]() x(x≥0),⊙E是以3为半径的圆,且圆心E在x轴上运动,若射线OP上存在点到⊙E的距离跨度为2,求出圆心E的横坐标xE的取值范围.
x(x≥0),⊙E是以3为半径的圆,且圆心E在x轴上运动,若射线OP上存在点到⊙E的距离跨度为2,求出圆心E的横坐标xE的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
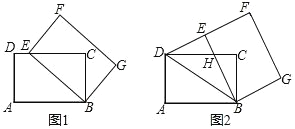
【题目】如图,在矩形 ABCD 中,AB=5,AD=3.以点 B 为中心,顺时针旋转矩形 BADC,得到矩形 BEFG,点 A、D、C 的对应点分别为 E、F、G.
(1)如图1,当点 E 落在 CD 边上时,求线段 CE 的长;
(2)如图2,当点 E 落在线段 DF 上时,求证:∠ABD=∠EBD;
(3)在(2)的条件下,CD 与 BE 交于点 H,求线段 DH 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
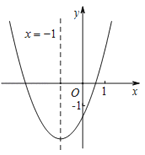
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为直线x=﹣1,与x轴的交点为(x1,0)、(x2,0),其中0<x1<1,有下列结论:①abc>0;②﹣3<x2<﹣2;③4a﹣2b+c<﹣1;④当m为任意实数时,a﹣b<am2+bm;⑤若点(﹣0.5,y1),(﹣2,y2)均在抛物线上,则y1>y2;⑥a>![]() .其中,正确结论的个数为( )
.其中,正确结论的个数为( )
A.2B.3C.4D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com