
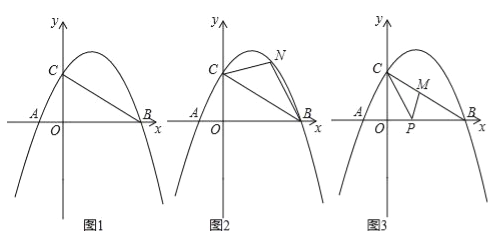
【题目】如图1,抛物线y=﹣![]() [(x﹣2)2+n]与x轴交于点A(m﹣2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连结BC.
[(x﹣2)2+n]与x轴交于点A(m﹣2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连结BC.
(1)求m、n的值;
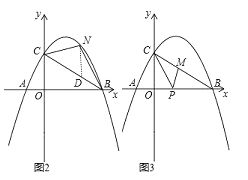
(2)如图2,点N为抛物线上的一动点,且位于直线BC上方,连接CN、BN.求△NBC面积的最大值;
(3)如图3,点M、P分别为线段BC和线段OB上的动点,连接PM、PC,是否存在这样的点P,使△PCM为等腰三角形,△PMB为直角三角形同时成立?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)m=1,n=﹣9;(2)![]() ;(3)存在,P点坐标为(
;(3)存在,P点坐标为(![]() ,0)或(
,0)或(![]() ,0).
,0).
【解析】
(1)利用抛物线的解析式确定对称轴为直线x=2,再利用对称性得到2﹣(m﹣2)=2m+3﹣2,解方程可得m的值,从而得到A(﹣1,0),B(5,0),然后把A点坐标代入y=﹣![]() [(x﹣2)2+n]可求出n的值;
[(x﹣2)2+n]可求出n的值;
(2)作ND∥y轴交BC于D,如图2,利用抛物线解析式确定C(0,3),再利用待定系数法求出直线BC的解析式为y=﹣![]() x+3,设N(x,﹣
x+3,设N(x,﹣![]() x2+
x2+![]() x+3),则D(x,﹣
x+3),则D(x,﹣![]() x+3),根据三角形面积公式,利用S△NBC=S△NDC+S△NDB可得S△BCN=﹣
x+3),根据三角形面积公式,利用S△NBC=S△NDC+S△NDB可得S△BCN=﹣![]() x2+
x2+![]() x,然后利用二次函数的性质求解;
x,然后利用二次函数的性质求解;
(3)先利用勾股定理计算出BC=![]() ,再分类讨论:当∠PMB=90°,则∠PMC=90°,△PMC为等腰直角三角形,MP=MC,设PM=t,则CM=t,MB=
,再分类讨论:当∠PMB=90°,则∠PMC=90°,△PMC为等腰直角三角形,MP=MC,设PM=t,则CM=t,MB=![]() ﹣t,证明△BMP∽△BOC,利用相似比可求出BP的长,再计算OP后可得到P点坐标;当∠MPB=90°,则MP=MC,设PM=t,则CM=t,MB=
﹣t,证明△BMP∽△BOC,利用相似比可求出BP的长,再计算OP后可得到P点坐标;当∠MPB=90°,则MP=MC,设PM=t,则CM=t,MB=![]() ﹣t,证明△BMP∽△BCO,利用相似比可求出BP的长,再计算OP后可得到P点坐标.
﹣t,证明△BMP∽△BCO,利用相似比可求出BP的长,再计算OP后可得到P点坐标.
解:(1)∵抛物线的解析式为y=﹣![]() [(x﹣2)2+n]=﹣
[(x﹣2)2+n]=﹣![]() (x﹣2)2﹣
(x﹣2)2﹣![]() n,
n,
∴抛物线的对称轴为直线x=2,
∵点A和点B为对称点,
∴2﹣(m﹣2)=2m+3﹣2,解得m=1,
∴A(﹣1,0),B(5,0),
把A(﹣1,0)代入y=﹣![]() [(x﹣2)2+n]得9+n=0,解得n=﹣9;
[(x﹣2)2+n]得9+n=0,解得n=﹣9;
(2)作ND∥y轴交BC于D,如图2,
抛物线解析式为y=﹣![]() [(x﹣2)2﹣9]=﹣
[(x﹣2)2﹣9]=﹣![]() x2+
x2+![]() x+3,
x+3,
当x=0时,y=3,则C(0,3),
设直线BC的解析式为y=kx+b,
把B(5,0),C(0,3)代入得![]() ,解得
,解得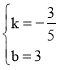 ,
,
∴直线BC的解析式为y=﹣![]() x+3,
x+3,
设N(x,﹣![]() x2+
x2+![]() x+3),则D(x,﹣
x+3),则D(x,﹣![]() x+3),
x+3),
∴ND=﹣![]() x2+
x2+![]() x+3﹣(﹣
x+3﹣(﹣![]() x+3)=﹣
x+3)=﹣![]() x2+3x,
x2+3x,
∴S△NBC=S△NDC+S△NDB=![]() 5ND=﹣
5ND=﹣![]() x2+
x2+![]() x=﹣(x﹣
x=﹣(x﹣![]() )2+
)2+![]() ,
,
当x=![]() 时,△NBC面积最大,最大值为
时,△NBC面积最大,最大值为![]() ;
;
(3)存在.
∵B(5,0),C(0,3),/p>
∴由勾股定理得BC=![]() ,
,
当∠PMB=90°,则∠PMC=90°,△PMC为等腰直角三角形,MP=MC,
设PM=t,则CM=t,MB=![]() ﹣t,
﹣t,
∵∠MBP=∠OBC,
∴△BMP∽△BOC,
∴![]() ,即
,即![]() ,解得t=
,解得t=![]() ,BP=
,BP=![]() ,
,
∴OP=OB﹣BP=5﹣![]() ,
,
此时P点坐标为(![]() ,0);
,0);
当∠MPB=90°,则MP=MC,
设PM=t,则CM=t,MB=![]() ﹣t,
﹣t,
∵∠MBP=∠CBO,
∴△BMP∽△BCO,
∴![]() ,即
,即![]() ,解得t=
,解得t=![]() ,BP=
,BP=![]() ,
,
∴OP=OB﹣BP=5﹣![]() ,
,
此时P点坐标为(![]() ,0);
,0);
综上所述,P点坐标为(![]() ,0)或(
,0)或(![]() ,0).
,0).


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】《孙子算经》内容主要讲数学的用途,浅显易懂,其中有许多有趣的数学题,如“河边洗碗”.原文:今有妇人河上荡桮.津吏问曰:“桮何以多?“妇人曰:“家有客.”津吏曰:“客几何?”妇人日:“二人共饭,三人共羹,四人共肉,凡用桮六十五.不知客几何?“译文:有一名妇女在河边洗刷一大摞碗.一个津吏问她:“怎么刷这么多碗呢?“她回答:“家里来客人了.“津吏又问:“家里来了多少客人?”妇女答道:“2个人给一碗饭,3个人给一碗汤,4个人给一碗肉,一共要用65只碗,来了多少客人?”答:共有_____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校开展“书香校园”活动以来,受到同学们的广泛关注,学校为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如图不完整的统计表.
学生借阅图书的次数:
借阅图书的次数 | 0次 | 1次 | 2次 | 3次 | 4次以上 |
人数 | 7 | 13 |
| 10 | 3 |

请你根据统计图表中的信息,解答下列问题:
(1)![]() ____________,
____________,![]() ____________;
____________;
(2)该调查统计数据的中位数是___________次;
(3)扇形统计图中,“3次”所对应扇形的圆心角的度数是____________;
(4)若该校共有2000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至G,使EG=AE,连接CG.
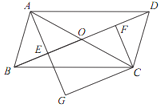
(1)求证:△ABE≌△CDF;
(2)当AB与AC满足什么数量关系时,四边形EGCF是矩形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中①△ABD≌△BCF;②四边形BDEF是平行四边形;③S四边形BDEF=![]() ;④S△AEF=
;④S△AEF=![]() .其中正确的有( )
.其中正确的有( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
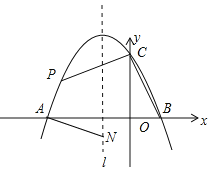
【题目】如图,抛物线![]() 与x轴交于点
与x轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,其对称轴1为
,其对称轴1为![]() .
.
(1)求抛物线的解析式并写出其顶点坐标;
(2)若动点![]() 在第二象限内的抛物线上,动点
在第二象限内的抛物线上,动点![]() 在对称轴1上.
在对称轴1上.
①当![]() ,且
,且![]() 时,求此时点
时,求此时点![]() 的坐标;
的坐标;
②当四边形![]() 的面积最大时,求四边形
的面积最大时,求四边形![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
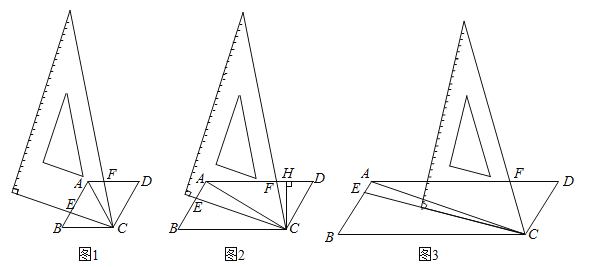
【题目】数学活动课上,某学习小组对有一内角为120°的平行四边形ABCD(∠BAD=120°)进行探究:将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB,AD于点E,F(不包括线段的端点).
(1)初步尝试
如图1,若AD=AB,求证:①△BCE≌△ACF,②AE+AF=AC;
(2)类比发现
如图2,若AD=2AB,过点C作CH⊥AD于点H,求证:AE=2FH;
(3)深入探究
如图3,若AD=3AB,探究得:![]() 的值为常数t,则t=____.
的值为常数t,则t=____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com