
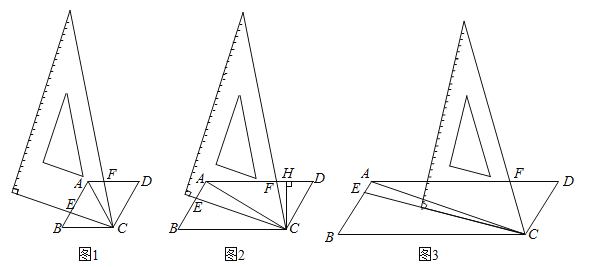
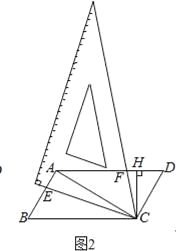
【题目】数学活动课上,某学习小组对有一内角为120°的平行四边形ABCD(∠BAD=120°)进行探究:将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB,AD于点E,F(不包括线段的端点).
(1)初步尝试
如图1,若AD=AB,求证:①△BCE≌△ACF,②AE+AF=AC;
(2)类比发现
如图2,若AD=2AB,过点C作CH⊥AD于点H,求证:AE=2FH;
(3)深入探究
如图3,若AD=3AB,探究得:![]() 的值为常数t,则t=____.
的值为常数t,则t=____.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)①先证明△ABC,△ACD都是等边三角形,再证明∠BCE=∠ACF即可解决问题.②根据①的结论得到BE=AF,由此即可证明.(2)设DH=x,由由题意,CD=2x,CH=![]() x,由△ACE∽△HCF,得
x,由△ACE∽△HCF,得![]()
![]()
由此即可证明;(3)如图3中,作CN⊥AD于N,CM⊥BA于M,CM与AD交于点H.先证明△CFN∽△CEM,得![]() ,由ABCM=ADCN,AD=3AB,推出CM=3CN,所以
,由ABCM=ADCN,AD=3AB,推出CM=3CN,所以![]() ,设CN=a,FN=b,则CM=3a,EM=3b,想办法求出AC,AE+3AF即可解决问题.
,设CN=a,FN=b,则CM=3a,EM=3b,想办法求出AC,AE+3AF即可解决问题.
解:(1)①∵四边形ABCD是平行四边形,∠BAD=120°,
∴∠D=∠B=60°, ∵AD=AB,
∴△ABC,△ACD都是等边三角形,
∴∠B=∠CAD=60°,∠ACB=60°,BC=AC,
∵∠ECF=60°,
∴∠BCE+∠ACE=∠ACF+∠ACE=60°, ∴∠BCE=∠ACF,
在△BCE和△ACF中,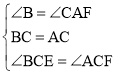
∴△BCE≌△ACF.
②∵△BCE≌△ACF,
∴BE=AF,
∴AE+AF=AE+BE=AB=AC.
(2)设DH=x,由由题意,CD=2x,CH=![]() x,
x,
∴AD=2AB=4x, ∴AH=AD﹣DH=3x,
∵CH⊥AD,
∴AC=![]() =2
=2![]() x,
x,
∴AC2+CD2=AD2, ∴∠ACD=90°, ∴∠BAC=∠ACD=90°, ∴∠CAD=30°,
∴∠ACH=60°,
∵∠ECF=60°,
∴∠HCF=∠ACE, ∴△ACE∽△HCF, ∴![]() =2,
=2,
∴AE=2FH.
(3)如图3中,作CN⊥AD于N,CM⊥BA于M,CM与AD交于点H.
∵∠ECF+∠EAF=180°,
∴∠AEC+∠AFC=180°,
∵∠AFC+∠CFN=180°,
∴∠CFN=∠AEC,
∵∠M=∠CNF=90°, ∴△CFN∽△CEM,
∴![]() , ∵ABCM=ADCN,AD=3AB, ∴CM=3CN,
, ∵ABCM=ADCN,AD=3AB, ∴CM=3CN,
∴![]() ,设CN=a,FN=b,则CM=3a,EM=3b,
,设CN=a,FN=b,则CM=3a,EM=3b,
∵∠MAH=60°,∠M=90°, ∴∠AHM=∠CHN=30°, ∴HC=2a,HM=a,HN=![]() a,
a,
∴AM=![]() a,AH=
a,AH=![]() a, ∴AC=
a, ∴AC=![]() a,
a,
AE+3AF=(EM﹣AM)+3(AH+HN﹣FN)=EM﹣AM+3AH+3HN﹣3FN=3AH+3HN﹣AM=![]() a,
a,
∴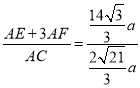 =
=![]()



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
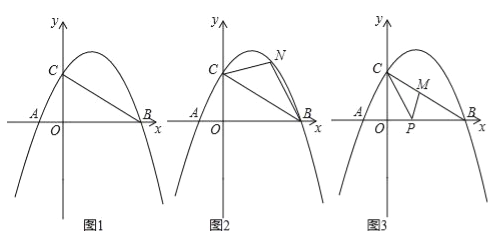
【题目】如图1,抛物线y=﹣![]() [(x﹣2)2+n]与x轴交于点A(m﹣2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连结BC.
[(x﹣2)2+n]与x轴交于点A(m﹣2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连结BC.
(1)求m、n的值;
(2)如图2,点N为抛物线上的一动点,且位于直线BC上方,连接CN、BN.求△NBC面积的最大值;
(3)如图3,点M、P分别为线段BC和线段OB上的动点,连接PM、PC,是否存在这样的点P,使△PCM为等腰三角形,△PMB为直角三角形同时成立?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,根据题意得( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地如图,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数图象;折线BCD表示轿车离甲地距离y(千米)与时间x(小时)之间的函数图象;请根据图象解答下到问题:
(1)货车离甲地距离y(干米)与时间x(小时)之间的函数式为 ;
(2)当轿车与货车相遇时,求此时x的值;
(3)在两车行驶过程中,当轿车与货车相距20千米时,求x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
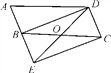
【题目】如图,将□ABCD的边AB延长至点E,使AB=BE,连接BD,DE,EC,DE交BC于点O.
(1)求证:△ABD≌△BEC;
(2)若∠BOD=2∠A,求证:四边形BECD是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个两位数,用![]() 表示十位上的数,用
表示十位上的数,用![]() 表示个位上的数.
表示个位上的数.
(1)用含![]() ,
,![]() 的式子表示这个两位数;
的式子表示这个两位数;
(2)把这个两位数个位上的数字与十位上的数字交换位置,得到一个新的两位数.
①若原数个位上的数是十位上的数的3倍,且新数与原数的差是36,求原来的两位数是多少?
②列式表示所得新数的平方与原数的平方的差(结果要化简),并判断其是11的倍数吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
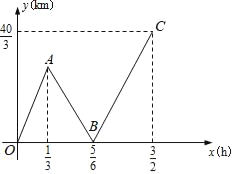
【题目】甲骑电动车、乙骑摩托车都从M地出发,沿一条笔直的公路匀速前往N地,甲先出发一段时间后乙再出发.甲,乙两人到达N地后均停止骑行,已知M,N两地相距![]() km,设甲行驶的时间为x(h),甲、乙两人之同的距离为y(km),表示y与x函数关系的图象如图所示.请你解决以下问题:
km,设甲行驶的时间为x(h),甲、乙两人之同的距离为y(km),表示y与x函数关系的图象如图所示.请你解决以下问题:
(1)求线段BC所在直线的函数表达式;
(2)分别求甲,乙的速度;
(3)填空:点A的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过
经过![]() 三点,已知
三点,已知![]()

![]() 求此抛物线的关系式;
求此抛物线的关系式;
![]() 设点
设点![]() 是线段
是线段![]() 上方的抛物线上一动点,过点
上方的抛物线上一动点,过点![]() 作
作![]() 轴的平行线,交线段
轴的平行线,交线段![]() 于点
于点![]() 当
当![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标;
的坐标;
![]() 点
点![]() 是抛物线上的一动点,当
是抛物线上的一动点,当![]() 中
中![]() 的面积最大时,请直接写出使
的面积最大时,请直接写出使![]() 的点
的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在长方形的边上.
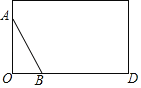
(1)用圆规和无刻度的直尺在长方形的内部作∠ABC=∠ABO;(保留作图痕迹,不写作法)
(2)在(1)的条件下,若BE是∠CBD的角平分线,探索AB与BE的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com