
【题目】在Rt△ABC中,∠A=30°,在AB边上取点D,以BD为直径作⊙O,与AC边切于点F,交BC边于点E.
(1)若BC=3,求⊙O的半径;
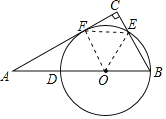
(2)①连接OF、EF,则四边形OFEB的形状为 ;
②写出你的推断过程.
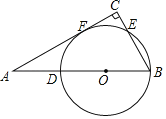
【答案】(1)2;(2)①菱形;②证明详见解析.
【解析】
(1)连接OF,根据直角三角形的性质求出AB,证明△AOF∽△ABC,根据相似三角形的性质得到![]() =
=![]() ,代入计算得到答案;
,代入计算得到答案;
(2)①根据图形猜想即可;
②根据等边三角形的判定定理得到△BOE为等边三角形,得到BE=OB=OE,根据菱形的判定定理证明结论.
解:(1)连接OF,
在Rt△ABC中,∠A=30°,
∴AB=2BC=6,
∵AC是⊙O的切线,
∴OF⊥AC,又BC⊥AC,
∴OF∥BC,
∴△AOF∽△ABC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,OF=2,即⊙O的半径为2;
(2)①四边形OFEB的形状为菱形,
故答案为:菱形;
②在Rt△ABC中,∠A=30°,
∴∠B=60°,
∵OB=OE,∠B=60°,
∴△BOE为等边三角形,
∴BE=OB=OE,
∵OF∥BC,BE=OF,
∴四边形OFBE为平行四边形,
∵BE=OB,
∴四边形OFEB的形状为菱形.


科目:初中数学 来源: 题型:
【题目】现有7张下面分别标有数字-2,-1,0,1,2,3,4的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任取一张,将该卡片上的数字记为m,则使得关于x的二次函数y=x2-2x+m-2与x轴有交点,且交于x的分式方程![]() 有解的概率为___ .
有解的概率为___ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列两则材料,回答问题:
材料一:平面直角坐标系中,对点A(x1,y1),B(x2,y2)定义一种新的运算:AB=x1x2+y1y2,例如:若A(1,2),B(3,4),则AB=1×3+2×4=11
材料二:平面直角坐标系中,过横坐标不同的两点A(x1,y1),B(x2,y2)的直线的斜率为kAB=![]() ,由此可以发现:若kAB=
,由此可以发现:若kAB=![]() =1,则有y1﹣y2=x1﹣x2,即x1﹣y1=x2﹣y2,反之,若x1,x2,y1,y2,满足关系式x1﹣y1=x2﹣y2,则有y1﹣y2=x1﹣x2,那么kAB=
=1,则有y1﹣y2=x1﹣x2,即x1﹣y1=x2﹣y2,反之,若x1,x2,y1,y2,满足关系式x1﹣y1=x2﹣y2,则有y1﹣y2=x1﹣x2,那么kAB=![]() =1.
=1.
(1)已知点M(﹣2,﹣6),N(3,﹣2),则MN= ,若点A,B的坐标分别为(x1,y1),(x2,y2)(x1≠x2),且满足关系式2x1+y1=2x2+y2,那么kAB= ;
(2)如图,横坐标互不相同的三个点C,D,E满足CD=DE,且D点是直线y=x上第一象限内的点,点D到原点的距离为2![]() .过点D作DF∥y轴,交直线CE于点F,若DF=6,请结合图象,求直线CE、直线DF与两坐标轴围成的四边形面积.
.过点D作DF∥y轴,交直线CE于点F,若DF=6,请结合图象,求直线CE、直线DF与两坐标轴围成的四边形面积.
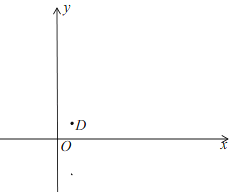
查看答案和解析>>
科目:初中数学 来源: 题型:
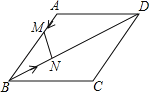
【题目】如图所示,菱形ABCD的边长是2厘米,∠BAD=120°,动点M以1厘米/秒的速度自A点出发向B移动,动点N以2厘米/移的速度自B点出发向D移动,两点中任一个到达线段端点移动便告结束.若点M、N同时出发运动了t秒,记△BMN的面积为S厘米2,下面图象中能表示S与t之间的函数关系的是( )
A.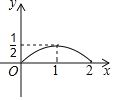 B.
B.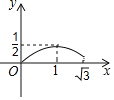
C.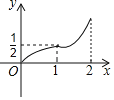 D.
D.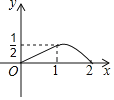
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中学生骑电动车上学给交通安全带来隐患,为了解某中学2 500个学生家长对“中学生骑电动车上学”的态度,从中随机调查400个家长,结果有360个家长持反对态度,则下列说法正确的是( )
A. 调查方式是普查 B. 该校只有360个家长持反对态度
C. 样本是360个家长 D. 该校约有90%的家长持反对态度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为( )
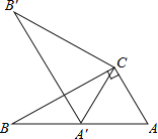
A.30°B.60°C.90°D.150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),其对称轴为直线x=1,下面结论中正确的有_____个.①abc>0,②2a﹣b=0,③4a+2b+c<0,④9a+3b+c=0
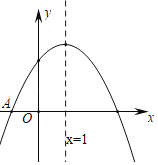
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1~4,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为S1,S2,S3,…,S10,则S1+S2+S3+…+S10= .
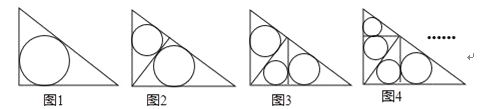
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com