
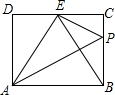
 如图,在矩形ABCD中,点E是CD的中点,AE平分∠BED,PE⊥AE交BC于点P,连接PA,以下四个结论:①BE平分∠AEC;②PA⊥BE;③AD=$\frac{\sqrt{3}}{2}$AB;④PB=2PC.则正确的个数是( )
如图,在矩形ABCD中,点E是CD的中点,AE平分∠BED,PE⊥AE交BC于点P,连接PA,以下四个结论:①BE平分∠AEC;②PA⊥BE;③AD=$\frac{\sqrt{3}}{2}$AB;④PB=2PC.则正确的个数是( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 根据矩形的性质结合全等三角形的判定与性质得出△ADE≌△BCE(SAS),进而求出△ABE是等边三角形,再求出△AEP≌△ABP(SSS),进而得出∠EAP=∠PAB=30°,分别的得出AD与AB,PB与PC的数量关系.
解答 解:∵在矩形ABCD中,点E是CD的中点,
∴DE=EC,
在△ADE和△BCE中
∵$\left\{\begin{array}{l}{AD=BC}\\{∠D=∠C}\\{DE=EC}\end{array}\right.$,
∴△ADE≌△BCE(SAS),
∴AE=BE,∠DEA=∠CEB,
∵AE平分∠BED,
∴∠AED=∠AEB,
∴∠AED=∠AEB=∠CEB=60°,
故:①BE平分∠AEC,正确;
可得△ABE是等边三角形,
∴∠DAE=∠EBC=30°,
∵PE⊥AE,
∴∠DEA+∠CEP=90°,
则∠CEP=30°,
故∠PEB=∠EBP=30°,
则EP=BP,
在△AEP和△ABP中
$\left\{\begin{array}{l}{AE=AB}\\{AP=AP}\\{EP=BP}\end{array}\right.$,
∴△AEP≌△ABP(SSS),
∴∠EAP=∠PAB=30°,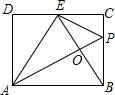
又∵AE=AB,
∴AP⊥BE,故②正确;
∵∠DAE=30°,
∴$\frac{DE}{AD}$=tan30°=$\frac{\sqrt{3}}{3}$,
∴3DE=$\sqrt{3}$AD,
∴AD=$\sqrt{3}$DE,
∴③AD=$\frac{\sqrt{3}}{2}$AB正确;
∵∠CEP=30°,
∴CP=$\frac{1}{2}$EP,
∵EP=BP,
∴CP=$\frac{1}{2}$BP,
∴④PB=2PC正确.
总上所述:正确的共有4个.
故选:A.
点评 此题主要考查了四边形综合以及全等三角形的判定与性质以及等边三角形的判定与性质和等腰三角形的性质等知识,正确得出△AEP≌△ABP是解题关键.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
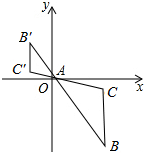 如图,△ABC在平面直角坐标系中,A(1,0),B(m,n),以点A为位似中心,在点A的异侧作△ABC位似图形△AB′C′.已知△ABC与△AB′C′的位似比为2:1,则点B′的坐标为( )
如图,△ABC在平面直角坐标系中,A(1,0),B(m,n),以点A为位似中心,在点A的异侧作△ABC位似图形△AB′C′.已知△ABC与△AB′C′的位似比为2:1,则点B′的坐标为( )| A. | ($\frac{m}{2}$,$\frac{n}{2}$) | B. | (-$\frac{m}{2}$,-$\frac{n}{2}$) | C. | ($\frac{m-3}{2}$,$\frac{n}{2}$) | D. | (-$\frac{m-3}{2}$,-$\frac{n}{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
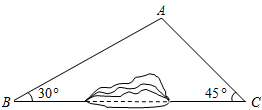 如图所示,因B、C两地之间有一座小山丘阻挡,故无法直接通车.现从B地需经A地才能到达C地.若B、C两地相距6000m,公路AB与BC夹角约为30°,公路AC与BC夹角约为45°,请计算路线B→A→C比BC远了多少米?(参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,结果保留整数)
如图所示,因B、C两地之间有一座小山丘阻挡,故无法直接通车.现从B地需经A地才能到达C地.若B、C两地相距6000m,公路AB与BC夹角约为30°,公路AC与BC夹角约为45°,请计算路线B→A→C比BC远了多少米?(参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,结果保留整数)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com