
分析 (1)先配方,然后利用非负数的性质即可解决.
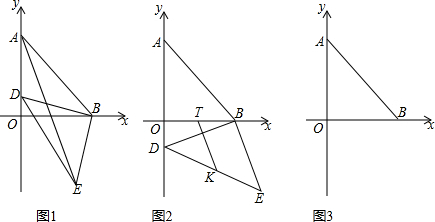
(2)如图1中,作EG⊥OB于G,先证明△DBO≌△BEG,得DO=BG,BO=EG,推出AD=OG,再证明△AOM≌△EGM得OM=MG,由此可以解决问题.
(3)如图3中,过点B作x轴的垂线交DT于H,连接EH,先证明△DOT≌△HBT得DO=BH=BM,DT=TH,再证明△DBM≌△EBH,DM=EH,结合条件推出TK=$\frac{1}{2}$EH=$\frac{1}{2}$DM,欲求TK的最小值,只要求出DM的最小值,设OP=x,则OM=2-x,DM=$\sqrt{{x}^{2}+(2-x)^{2}}$=$\sqrt{2(x-1)^{2}+2}$,根据二次函数的性质即可解决问题.
解答 (1)解:∵4a2-2ab+b2-12a+12=0,
∴(a-b)2+3(a-2)2=0,
∵(a-b)2≥0,3(a-2)2≥0,
∴a=b=2,
∴点A坐标(0,2),点B坐标(2,0).
(2)解:如图1中,作EG⊥OB于G,
∵△BDE为等腰直角三角形,∠DBE=90°,
∴BD=BE,∠DBO+∠OBE=90°,
∵EG⊥BO,
∴∠OBE+∠BEG=90°,
∴∠DBO=∠BEG,
在△DBO和△BEG中,
$\left\{\begin{array}{l}{∠DOB=∠EGM}\\{∠OBD=∠BEG}\\{BD=BE}\end{array}\right.$,
∴△DBO≌△BEG,
∴DO=BG,BO=EG,
∵AO=BO,
∴AO=EG,AD=OG,
在△AOM和△EGM中,
$\left\{\begin{array}{l}{∠AOM=∠EGM}\\{∠AMO=∠EMG}\\{AO=EG}\end{array}\right.$,
∴△AOM≌△EGM,
∴OM=MG,
∴$\frac{OM}{AD}$=2.
(3)解:如图3中,过点B作x轴的垂线交DT于H,连接EH,
在△DOT和△HBT中,
$\left\{\begin{array}{l}{∠DOT=∠HBT}\\{∠DTO=∠HTB}\\{OT=TB}\end{array}\right.$,
∴△DOT≌△HBT,
∴DO=BH=BM,DT=TH,
∵∠DBE=∠OBH,
∴∠DBM=∠EBH,
在△DBM和△EBH中,
$\left\{\begin{array}{l}{DB=EB}\\{∠DBM=∠EBH}\\{BM=BH}\end{array}\right.$,
∴△DBM≌△EBH,
∴DM=EH,
∵DK=KE,DT=TH,
∴TK=$\frac{1}{2}$EH=$\frac{1}{2}$DM,
∵DO+OM=2,设OP=x,则OM=2-x,DM=$\sqrt{{x}^{2}+(2-x)^{2}}$=$\sqrt{2(x-1)^{2}+2}$,
∴x=1时,DM最小即TK最小,此时点D坐标(0,1).
点评 本题考查全等三角形的判定和性质、等腰三角形的性质、二次函数的性质,综合性比较强,解题的关键是添加辅助线构造全等三角形,学会转化的思想,最小值问题想到用二次函数解决,属于中考压轴题.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
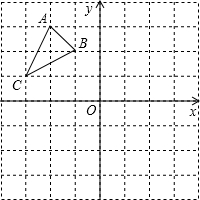 如图,在边长为1的正方形组成的网格中,△ABC的顶点均在格点上,点A、B、C的坐标分别是A(-2,3)、B(-1,2)、C(-3,1),△ABC绕点O顺时针旋转90°后得到△A1B1C1.
如图,在边长为1的正方形组成的网格中,△ABC的顶点均在格点上,点A、B、C的坐标分别是A(-2,3)、B(-1,2)、C(-3,1),△ABC绕点O顺时针旋转90°后得到△A1B1C1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
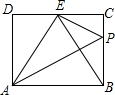 如图,在矩形ABCD中,点E是CD的中点,AE平分∠BED,PE⊥AE交BC于点P,连接PA,以下四个结论:①BE平分∠AEC;②PA⊥BE;③AD=$\frac{\sqrt{3}}{2}$AB;④PB=2PC.则正确的个数是( )
如图,在矩形ABCD中,点E是CD的中点,AE平分∠BED,PE⊥AE交BC于点P,连接PA,以下四个结论:①BE平分∠AEC;②PA⊥BE;③AD=$\frac{\sqrt{3}}{2}$AB;④PB=2PC.则正确的个数是( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com