
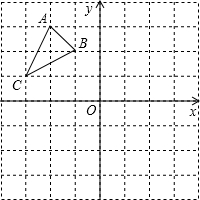
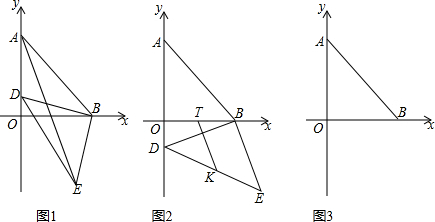
 ��ͼ���ڱ߳�Ϊ1����������ɵ������У���ABC�Ķ�����ڸ���ϣ���A��B��C������ֱ���A��-2��3����B��-1��2����C��-3��1������ABC�Ƶ�O˳ʱ����ת90���õ���A1B1C1��
��ͼ���ڱ߳�Ϊ1����������ɵ������У���ABC�Ķ�����ڸ���ϣ���A��B��C������ֱ���A��-2��3����B��-1��2����C��-3��1������ABC�Ƶ�O˳ʱ����ת90���õ���A1B1C1������ ��1�����������ص����ת�����ʻ�����A��B��C�Ķ�Ӧ��A1��B1��C1���Ӷ��õ���A1B1C1��
��2�����ڵ�C������·������O��ΪԲ�ģ�OCΪ�뾶��Բ�Ľ�Ϊ90�ȵĻ����������û�����ʽ�ɼ������C������·��$\widehat{C{C}_{1}}$�ij��ȣ�
��3���������ۣ���B�����y��ĶԳƵ�B�䣬����CB�佻y����D����ͼ2����B�䣨1��2������������֮���߶���̿��жϴ�ʱDB+DB��С�����ô���ϵ���������ֱ��CB��Ľ���ʽ��Ȼ�����ֱ����y��Ľ��㼴�ɣ���C�����x��ĶԳƵ�C�䣬����C��B��x����D�䣬��ͼ2����C�䣨-3��-1�������ô���ϵ���������ֱ��C��B�Ľ���ʽ��Ȼ�����ֱ����x��Ľ��㼴�ɣ�
��� �⣺��1����ͼ1����A1B1C1Ϊ������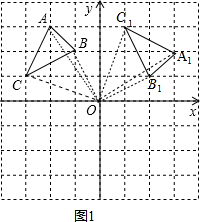
��2��OC=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$��
���Ե�C������·��$\widehat{C{C}_{1}}$�ij���=$\frac{90•��•\sqrt{10}}{180}$=$\frac{\sqrt{10}}{2}$�У�
��3����B�����y��ĶԳƵ�B�䣬����CB�佻y����D����ͼ2����B�䣨1��2����
��DB+DC=DB��+DC=CB�䣬
���ʱDB+DB��С��
��ֱ��CB��Ľ���ʽΪy=mx+n��
��C��-3��1����B�䣨1��2�������$\left\{\begin{array}{l}{-3k+b=1}\\{k+b=2}\end{array}\right.$�����$\left\{\begin{array}{l}{k=\frac{1}{4}}\\{b=\frac{7}{4}}\end{array}\right.$��
����ֱ��CB��Ľ���ʽΪy=$\frac{1}{4}$x+$\frac{7}{4}$��
��x=0ʱ��y=$\frac{1}{4}$x+$\frac{7}{4}$=$\frac{7}{4}$��
��D��0��$\frac{7}{4}$����
��C�����x��ĶԳƵ�C�䣬����C��B��x����D�䣬��ͼ2����C�䣨-3��-1����
��D��B+D��C=D��B+D��C��=C��B��
���ʱD��B+D��B����С��
��ֱ��C��B�Ľ���ʽΪy=px+q��
��C�䣨-3��-1����B��-1��2�������$\left\{\begin{array}{l}{-3p+q=-1}\\{-p+q=2}\end{array}\right.$�����$\left\{\begin{array}{l}{p=\frac{3}{2}}\\{q=\frac{7}{2}}\end{array}\right.$��
����ֱ��C��B�Ľ���ʽΪy=$\frac{3}{2}$x+$\frac{7}{2}$��
��y=0ʱ��$\frac{3}{2}$x+$\frac{7}{2}$=0�����x=-$\frac{7}{3}$��
��D�䣨-$\frac{7}{3}$��0����
����������D����������0��$\frac{7}{4}$����-$\frac{7}{3}$��0����
�ʴ�Ϊ$\frac{\sqrt{10}}{2}$�У���0��$\frac{7}{4}$����-$\frac{7}{3}$��0����
���� ���⿼������ͼ-��ת�任��������ת�����ʿ�֪����Ӧ�Ƕ���ȶ�������ת�ǣ���Ӧ�߶�Ҳ��ȣ��ɴ˿���ͨ������ȵĽǣ��ڽǵı��Ͻ�ȡ��ȵ��߶εķ������ҵ���Ӧ�㣬˳�����ӵó���ת���ͼ�Σ�Ҳ�����˻�����ʽ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����һ��ֱ�����ǰ��ֱ�Ƕ������ֱ�ߵ�һ���ϣ�����1=25�㣬���2�Ķ���Ϊ��������
��ͼ����һ��ֱ�����ǰ��ֱ�Ƕ������ֱ�ߵ�һ���ϣ�����1=25�㣬���2�Ķ���Ϊ��������| A�� | 25�� | B�� | 65�� | C�� | 55�� | D�� | 40�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
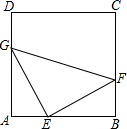 ��ͼ��������ABCD�У���E��F��G�ֱ�Ϊ��AB��BC��AD�ϵĵ㣬��AE=BF=DG������EF��GE��GF��
��ͼ��������ABCD�У���E��F��G�ֱ�Ϊ��AB��BC��AD�ϵĵ㣬��AE=BF=DG������EF��GE��GF���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com