
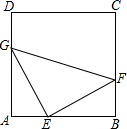
 如图,正方形ABCD中,点E,F,G分别为边AB,BC,AD上的点,且AE=BF=DG,连接EF,GE,GF.
如图,正方形ABCD中,点E,F,G分别为边AB,BC,AD上的点,且AE=BF=DG,连接EF,GE,GF.分析 (1)连接BD交GF于点M即可,根据题意确定旋转角;
(2)设正方形边长为a,AE=BF=DG=x,证明Rt△GAE和Rt△EBF,得到∠GEF是等腰直角三角形,根据三角形的面积公式列出二次函数解析式,根据二次函数的性质得到答案;
(3)分点E位于AB的中点和点E位于AB的非中点两种情况,根据直线与圆的位置关系的确定方法解得即可.
解答 解:(1)如图1,连接BD交GF于点M,则点M即为所求,
旋转α=∠AMB=90°;
(2)当点E位于AB的中点时,△EFG面积取得最小值.
理由如下:设正方形边长为a,AE=BF=DG=x,
则AG=a-x,
在Rt△GAE中,GE2=AG2+AE2=(a-x)2+x2=2x2-2ax+a2,
在Rt△GAE和Rt△EBF中,
$\left\{\begin{array}{l}{GA=EB}\\{∠DAB=∠ABC}\\{AE=BF}\end{array}\right.$,
∴Rt△GAE和Rt△EBF,
∴GE=FE,∠AEG=∠BFE,
∴∠GEF是等腰直角三角形,
∴△EFG的面积=$\frac{1}{2}$GE2=(x-$\frac{1}{2}$a)2+$\frac{1}{4}$a2,
所以当x=$\frac{1}{2}$a,即点E位于AB的中点时,△EFG面积取得最小值;
(3)当点E位于AB的中点时,
直线CD与△EFG的外接圆相切,
理由:GF的中点为O,连接EO,
则EO=$\frac{1}{2}$GF,
当点E位于AB的中点时,点G位于AD的中点,点F位于CB的中点,
则GF=CD=AD,
∴EO=$\frac{1}{2}$AD,
∴当O到CD的距离为$\frac{1}{2}$AD,
∴直线CD与△EFG的外接圆相切;
当点E位于AB的非中点时,直线CD与△EFG的外接圆相交,
理由:当点E位于AB的非中点时,GF>CD,
∴O到CD的距离<OE,
∴直线CD与△EFG的外接圆相交.
点评 本题考查的是正方形的性质、旋转的性质、二次函数的性质以及直线与圆的位置关系,正确根据题意列出二次函数解析式是解题的关键,注意等腰直角三角形的判定和直角三角形的性质的灵活运用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
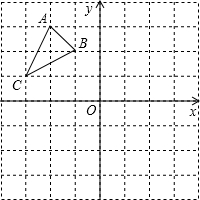 如图,在边长为1的正方形组成的网格中,△ABC的顶点均在格点上,点A、B、C的坐标分别是A(-2,3)、B(-1,2)、C(-3,1),△ABC绕点O顺时针旋转90°后得到△A1B1C1.
如图,在边长为1的正方形组成的网格中,△ABC的顶点均在格点上,点A、B、C的坐标分别是A(-2,3)、B(-1,2)、C(-3,1),△ABC绕点O顺时针旋转90°后得到△A1B1C1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
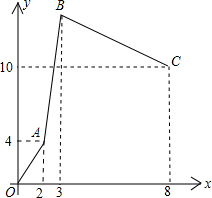 某仓库甲、乙、丙三辆运货车,每辆车只负责进货或出货,每小时的运输量丙车最多,乙车最少,乙车的运输量为每小时6吨,下图是从早晨上班开始库存量y(吨)与时间x(小时)的函数图象,OA段只有甲、丙车工作,AB段只有乙、丙车工作,BC段只有甲、乙工作.
某仓库甲、乙、丙三辆运货车,每辆车只负责进货或出货,每小时的运输量丙车最多,乙车最少,乙车的运输量为每小时6吨,下图是从早晨上班开始库存量y(吨)与时间x(小时)的函数图象,OA段只有甲、丙车工作,AB段只有乙、丙车工作,BC段只有甲、乙工作.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
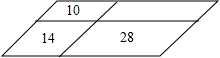 农业技术员在一块平行四边形的实验田里种植四种不同的农作物,现需将该实验田划成四个平行四边形地块(如图),已知其中三块田的面积分别是14m2,10m2,28m2,则第四块田的面积为20m2.
农业技术员在一块平行四边形的实验田里种植四种不同的农作物,现需将该实验田划成四个平行四边形地块(如图),已知其中三块田的面积分别是14m2,10m2,28m2,则第四块田的面积为20m2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 北京时间2015年04月25日14时11分,尼泊尔发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作.如图,某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=3米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,$\sqrt{3}$≈1.7)
北京时间2015年04月25日14时11分,尼泊尔发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作.如图,某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=3米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,$\sqrt{3}$≈1.7)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com