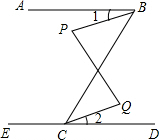
如图.已知∠ABC与∠ECB互补.∠1=∠2.∠P与∠Q一定相等吗?说说你的理由．题目和参考答案——青夏教育精英家教网—

18．

如图，已知∠ABC与∠ECB互补，∠1=∠2，∠P与∠Q一定相等吗？说说你的理由．

分析根据平行线的判定得出AB∥CD，根据平行线的性质得出∠1+∠PBC=∠2+∠QCB，求出∠PBC=∠QCB，根据三角形内角和定理求出即可．

解答解：∠P=∠Q，
理由是：∵∠ABC与∠ECB互补，
∴AB∥CD，
∴∠1+∠PBC=∠2+∠QCB，
∵∠1=∠2，
∴∠PBC=∠QCB，
∵∠POB+∠P+∠PBC=180°，∠COQ+∠QCB+∠Q=180°，∠POB=∠COQ，
∴∠P=∠Q．

点评本题考查了平行线的性质和判定，三角形内角和定理的应用，能求出∠PBC=∠QCB是解此题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

10．先化简，再求代数式$\frac{{b}^{2}-{a}^{2}}{{a}^{2}-ab}$÷（a+$\frac{2ab+{b}^{2}}{a}$）•（$\frac{1}{a}$+$\frac{1}{b}$）的值，其中a=2sin45°+tan60°，b=$\sqrt{2}$-2cos30°．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

11．计算：-2²+$\sqrt{（-2）^{2}}$+$\root{3}{-27}$+（3+π）⁰-|-3|．（提示：当a≠0时，a⁰=1）

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

6．若A（0，a）、B（b，0），且a、b满足4a²-2ab+b²-12a+12=0．
（1）求A、B的坐标．
（2）如图1，点D在线段AO上运动（不与点A、O重合），以BD为腰向下作等腰直角△BDE，∠DBE=90°，连接AE交BO于M，求$\frac{AD}{OM}$的值．
（3）如图2，点D在y轴上运动，以BD为腰向下作等腰直角△BDE，∠DBE=90°，K为DE中点，T为OB中点，当线段KT最短时，求此时D点坐标．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

13．

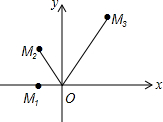如图，在平面直角坐标系中，已知点M₁（-1，0），将线段OM₁绕点O按顺时针方向旋转60°，再将其长度伸长为OM₁的2倍，得到线段OM₂；又将线段OM₂绕点O按顺时针方向旋转60°，长度伸长为OM₂的2倍，得到线段OM₃；如此下去，得到线段OM₄，OM₅…OM_n（n为正整数），则点M₂₃₄的坐标为（-2²³²，-2²³²•$\sqrt{3}$）．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

3．