
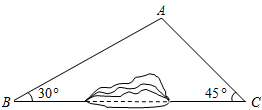
 如图所示,因B、C两地之间有一座小山丘阻挡,故无法直接通车.现从B地需经A地才能到达C地.若B、C两地相距6000m,公路AB与BC夹角约为30°,公路AC与BC夹角约为45°,请计算路线B→A→C比BC远了多少米?(参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,结果保留整数)
如图所示,因B、C两地之间有一座小山丘阻挡,故无法直接通车.现从B地需经A地才能到达C地.若B、C两地相距6000m,公路AB与BC夹角约为30°,公路AC与BC夹角约为45°,请计算路线B→A→C比BC远了多少米?(参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,结果保留整数) 分析 过A作AD⊥BC于D,在Rt△ACD中,解直角三角形求出AD的长度,然后在Rt△ABD中,求出AC+BC解答即可.
解答 解:过A作AD⊥BC于D,则BD=$\frac{AD}{tan30°}$,CD=$\frac{AD}{tan45°}$,
∵BD+CD=BC,
∴$(\sqrt{3}+1)AD=6000$,
∴AD=$3000(\sqrt{3}-1)$,
∴在Rt△ABD中,AB=6000$(\sqrt{3}-1)$,
在Rt△ACD中,AC=3000$(\sqrt{3}-1)•\sqrt{2}$,
∴AB+AC=6000$(\sqrt{3}-1)+3000(\sqrt{3}-1)×\sqrt{2}$≈7468(m),7468-6000=1468(m),
答:路线B→A→C比BC远了1468米.
点评 本题考查了解直角三角形的应用,难度适中,解答本题的关键是作三角形的高建立直角三角形幷解直角三角形.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
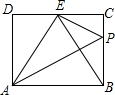 如图,在矩形ABCD中,点E是CD的中点,AE平分∠BED,PE⊥AE交BC于点P,连接PA,以下四个结论:①BE平分∠AEC;②PA⊥BE;③AD=$\frac{\sqrt{3}}{2}$AB;④PB=2PC.则正确的个数是( )
如图,在矩形ABCD中,点E是CD的中点,AE平分∠BED,PE⊥AE交BC于点P,连接PA,以下四个结论:①BE平分∠AEC;②PA⊥BE;③AD=$\frac{\sqrt{3}}{2}$AB;④PB=2PC.则正确的个数是( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
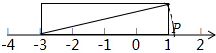 图中长方形的长为4个单位长度、宽为1个单位长度,则点P所表示的数为( )
图中长方形的长为4个单位长度、宽为1个单位长度,则点P所表示的数为( )| A. | $\sqrt{17}-3$ | B. | $\sqrt{17}$ | C. | -$\sqrt{17}+1$ | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
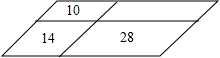 农业技术员在一块平行四边形的实验田里种植四种不同的农作物,现需将该实验田划成四个平行四边形地块(如图),已知其中三块田的面积分别是14m2,10m2,28m2,则第四块田的面积为20m2.
农业技术员在一块平行四边形的实验田里种植四种不同的农作物,现需将该实验田划成四个平行四边形地块(如图),已知其中三块田的面积分别是14m2,10m2,28m2,则第四块田的面积为20m2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | $-\frac{5}{13}$ | D. | $-\frac{13}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com