
已知二次函数y=x2+bx+c的图象经过(2,﹣1)和(4,3)两点,求二次函数y=x2+bx+c的表达式.
【考点】待定系数法求二次函数解析式.
【专题】计算题.
【分析】把(2,﹣1)和(4,3)代入y=x2+bx+c中得到关于b、c的方程组,然后解方程组即可.
【解答】解:把(2,﹣1)和(4,3)代入y=x2+bx+c得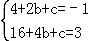 ,解得
,解得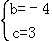 ,
,
所以二次函数解析式为y=x2﹣4x+3.
【点评】本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.


科目:初中数学 来源: 题型:
如果点M(﹣2,y1),N(﹣1,y2)在抛物线y=﹣x2+2x上,那么下列结论正确的是( )
A.y1<y2 B.y1>y2 C.y1≤y2 D.y1≥y2
查看答案和解析>>
科目:初中数学 来源: 题型:
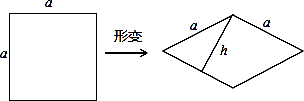
如图,边长为a的正方形发生形变后成为边长为a的菱形,如果这个菱形的一组对边之间的距离为h,记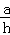 =k,我们把k叫做这个菱形的“形变度”.若变形后的菱形有一个角是60°,则形变度k= .
=k,我们把k叫做这个菱形的“形变度”.若变形后的菱形有一个角是60°,则形变度k= .
查看答案和解析>>
科目:初中数学 来源: 题型:
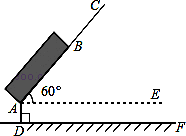
一种拉杆式旅行箱的示意图如图所示,箱体长AB=50cm,拉杆最大伸长距离BC=30cm,点A到地面的距离AD=8cm,旅行箱与水平面AE成60°角,求拉杆把手处C到地面的距离(精确到1cm).(参考数据: )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com