
分析 由1×2=$\frac{1}{3}$(1×2×3-0×1×2),2×3=$\frac{1}{3}$(2×3×4-1×2×3),3×4=$\frac{1}{3}$(3×4×5-2×3×4),…,得出n(n+1)=$\frac{1}{3}$[(n(n+1)(n+2)-(n-1)n(n+1)],由此规律进一步拆开抵消得出答案即可.
解答 解:(1)1×2+2×3+3×4+…+10×11
=$\frac{1}{3}$(1×2×3-0×1×2+2×3×4-1×2×3+…+10×11×12-9×10×11)
=$\frac{1}{3}$×10×11×12
=440.
(2)1×2+2×3+3×4+…+n×(n+1)
=$\frac{1}{3}$[1×2×3-0×1×2+2×3×4-1×2×3+…+n(n+1)(n+2)-(n-1)n(n+1)]
=$\frac{1}{3}$n(n+1)(n+2).
点评 此题主要考查数字的变化规律,通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题.


科目:初中数学 来源: 题型:选择题
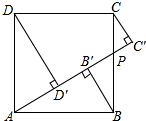 如图,正方形ABCD的边长为$\sqrt{2}$,点P为BC上任意一点(可与B点或C点重合),分别过B、C、D作射线AP的垂线,垂足分别是B′、C′、D′,则BB′+CC′+DD′的最大值为( )
如图,正方形ABCD的边长为$\sqrt{2}$,点P为BC上任意一点(可与B点或C点重合),分别过B、C、D作射线AP的垂线,垂足分别是B′、C′、D′,则BB′+CC′+DD′的最大值为( )| A. | $\frac{4}{3}\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 2 | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
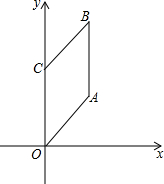 如图,在菱形OABC中,点O为坐标原点,点C在y轴上,且A(3,4).
如图,在菱形OABC中,点O为坐标原点,点C在y轴上,且A(3,4).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
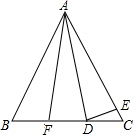 如图,△ABC中,∠B=∠C,AB=AC,D、F在BC边上,BF=CD,E在AC边上,∠ADE=∠AED,∠EDC=23°,则∠FAC=46°.
如图,△ABC中,∠B=∠C,AB=AC,D、F在BC边上,BF=CD,E在AC边上,∠ADE=∠AED,∠EDC=23°,则∠FAC=46°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com