
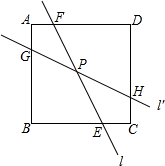
 如图,直线l经过正方形ABCD内一点P,并交边BC、DA于E、F两点,将直线l绕点P按逆时针方向旋转45°得到直线l′,并交边AB、CD于G、H两点.若AB=4,GH=2$\sqrt{5}$,则EF的值为$\frac{4\sqrt{10}}{3}$.
如图,直线l经过正方形ABCD内一点P,并交边BC、DA于E、F两点,将直线l绕点P按逆时针方向旋转45°得到直线l′,并交边AB、CD于G、H两点.若AB=4,GH=2$\sqrt{5}$,则EF的值为$\frac{4\sqrt{10}}{3}$. 分析 作AK∥EF交BC于K、作AM∥GH交CD于M,可得∠KAM=45°,作∠KAN=45°交CB延长线于点N,求出∠DAM=∠BAN,然后利用“ASA”证明△DAM≌△BAN,根据全等三角形对应边相等可得AM=AN、DM=BN,利用勾股定理求出DM,过点K作KP⊥AN于P,可得△KAP是等腰直角三角形,设AK=EF=x,表示出KP,然后利用∠N的正切值列出方程求解即可.
解答 解:如图,作AK∥EF交BC于K,作AM∥GH交CD于M,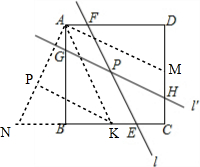
则AM=GH=2$\sqrt{5}$,AK=EF,
∵∠GPF=45°,
∴∠KAM=45°,
∴∠BAK+∠DAM=90°-45°=45°,
作∠KAN=45°交CB延长线于点N,则∠BAK+∠BAN=45°,
∴∠DAM=∠BAN,
在△DAM和△BAN中,
$\left\{\begin{array}{l}{∠DAM=∠BAN}\\{AD=AB}\\{∠D=∠ABN=90°}\end{array}\right.$,
∴△DAM≌△BAN(ASA),
∴AM=AN,DM=BN,
在RT△ADM中,DM=$\sqrt{A{M}^{2}-A{D}^{2}}$=$\sqrt{(2\sqrt{5})^{2}-{4}^{2}}$=2,
过点K作KP⊥AN于P,
∵∠KAP=45°,
∴△KAP是等腰直角三角形,
设AK=EF=x,则AP=KP=$\frac{\sqrt{2}}{2}$x,
∵tan∠N=$\frac{AB}{BN}=\frac{KP}{NP}$,
∴$\frac{4}{2}=\frac{\frac{\sqrt{2}}{2}x}{2\sqrt{5}-\frac{\sqrt{2}}{2}x}$,
解得:x=$\frac{4\sqrt{10}}{3}$,
所以EF=$\frac{4\sqrt{10}}{3}$.
故答案为:$\frac{4\sqrt{10}}{3}$.
点评 本题考查了正方形的性质,全等三角形的判定与性质,等腰直角三角形的性质,锐角三角函数的定义,熟记各性质并作辅助线构造出全等三角形和等腰直角三角形是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
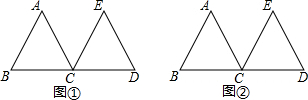 如图,等边△ABC和等边△ECD的边长相等,BC与CD在同一直线上,请根据如下要求,使用无刻度的直尺画图.
如图,等边△ABC和等边△ECD的边长相等,BC与CD在同一直线上,请根据如下要求,使用无刻度的直尺画图.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在平面直角坐标系中,点A(2,3),B(5,-2),以原点O为位似中心,位似比为1:2,把△ABO缩小,则点B的对应点B′的坐标是($\frac{5}{2}$,-1)或(-$\frac{5}{2}$,1).
在平面直角坐标系中,点A(2,3),B(5,-2),以原点O为位似中心,位似比为1:2,把△ABO缩小,则点B的对应点B′的坐标是($\frac{5}{2}$,-1)或(-$\frac{5}{2}$,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com