
【题目】如图①,直线AB的解析式为y=﹣![]() x+4,抛物线y=﹣
x+4,抛物线y=﹣![]() +bx+c与y轴交于点A,与x轴交于点C(6,0),点P是抛物线上一动点,设点P的横坐标为m.
+bx+c与y轴交于点A,与x轴交于点C(6,0),点P是抛物线上一动点,设点P的横坐标为m.
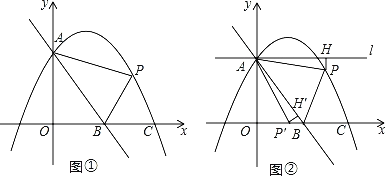
(1)求抛物线的解析式;
(2)当点P在第一象限内时,求△ABP面积的最大值,并求此时点P的坐标;
(3)如图②,当点P在y轴右侧时,过点A作直线l∥x轴,过点P作PH⊥l于点H,将△APH绕点A顺时针旋转,当点H的对应点H′恰好落在直线AB上时,点P的对应点P′恰好落在坐标轴上,请直接写出点P的横坐标.
【答案】(1)![]() ;(2)面积最大值为8,
;(2)面积最大值为8,![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)先利用直线进行确定则A(0,4),然后利用待定系数法求抛物线解析式;
(2)连接OP,设P(m,﹣![]() m2+
m2+![]() m+4),解方程﹣
m+4),解方程﹣![]() x+4=0得B(3,0),根据三角形面积公式,利用面积的和差得到S△ABP=S△AOP+S△POB﹣S△AOB=
x+4=0得B(3,0),根据三角形面积公式,利用面积的和差得到S△ABP=S△AOP+S△POB﹣S△AOB=![]() ×4m+
×4m+![]() ×3(﹣
×3(﹣![]() m2+
m2+![]() m+4)﹣
m+4)﹣![]() ×3×4,然后根据二次函数的性质解决问题;
×3×4,然后根据二次函数的性质解决问题;
(3)先利用勾股定理计算出AB=5,讨论:当点P′落在x轴上,如图2,根据旋转的性质得=4﹣(﹣![]() m2+
m2+![]() m+4)=
m+4)=![]() m2﹣
m2﹣![]() m,AH′=AH=m,∠P′H′A=∠PHA=90°,再证明△BP′H′∽△BAO,利用相似得到BH′=
m,AH′=AH=m,∠P′H′A=∠PHA=90°,再证明△BP′H′∽△BAO,利用相似得到BH′=![]() m2﹣m,然后利用AH′+BH′=AB得到m+
m2﹣m,然后利用AH′+BH′=AB得到m+![]() m2﹣m=5,解方程求出m即可得到P点横坐标;当点P′落在y轴上,如图3,同理可得P′H′=PH=
m2﹣m=5,解方程求出m即可得到P点横坐标;当点P′落在y轴上,如图3,同理可得P′H′=PH=![]() m2﹣
m2﹣![]() m,AH′=AH=m,∠P′H′A=∠PHA=90°,通过证明△AH′P′′∽△AOB,然后利用相似比得到(
m,AH′=AH=m,∠P′H′A=∠PHA=90°,通过证明△AH′P′′∽△AOB,然后利用相似比得到(![]() m2﹣
m2﹣![]() m):3=m:4,然后解关于m的方程即可得到对应P点横坐标.
m):3=m:4,然后解关于m的方程即可得到对应P点横坐标.
解:(1)当x=0时,y=﹣![]() x+4=4,则A(0,4),
x+4=4,则A(0,4),
∵抛物线y=﹣![]() x2+bx+c与y轴交于点A,与x轴交于点C(6,0),
x2+bx+c与y轴交于点A,与x轴交于点C(6,0),
∴![]() ,解得:
,解得:![]() ,
,
∴抛物线解析式为y=﹣![]() x2+
x2+![]() x+4;
x+4;
(2)连接OP,
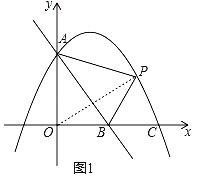
设P(m,﹣![]() m2+
m2+![]() m+4),
m+4),
当y=0时,﹣![]() x+4=0,解得x=3,
x+4=0,解得x=3,
则B(3,0),
∵S△ABP=S△AOP+S△POB﹣S△AOB=![]() ×4m+
×4m+![]() ×3(﹣
×3(﹣![]() m2+
m2+![]() m+4)﹣
m+4)﹣![]() ×3×4
×3×4
=﹣![]() m2+4m,
m2+4m,
=﹣![]() (m﹣4)2+8,
(m﹣4)2+8,
当m=4时,△ABP面积有最大值,最大值为8,此时P点坐标为(4,4);
(3)在Rt△OAB中,AB=![]() =
=![]() =5,
=5,
当点![]() 落在x轴上,如图2,
落在x轴上,如图2,
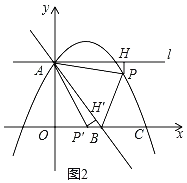
∵△APH绕点A顺时针旋转,使点H的对应点![]() 恰好落在直线AB上,同时
恰好落在直线AB上,同时![]() 恰好落在x轴上
恰好落在x轴上
∴![]() =PH=4﹣(﹣
=PH=4﹣(﹣![]() m2+
m2+![]() m+4)=
m+4)=![]() m2﹣
m2﹣![]() m,
m,![]() =AH=m,
=AH=m,![]() =∠PHA=90°,
=∠PHA=90°,
∵![]() =∠ABO,
=∠ABO,
∴![]() ∽△BAO,
∽△BAO,
∴![]() :OA=
:OA=![]() :OB,即(
:OB,即(![]() m2﹣
m2﹣![]() m):4=
m):4=![]() :3,
:3,
∴![]() =
=![]() m2﹣m,
m2﹣m,
∵![]() ,
,
∴m+![]() m2﹣m=5,
m2﹣m=5,
解得m1=2![]() ,m2=﹣2
,m2=﹣2![]() (舍去),
(舍去),
此时P点横坐标为2![]() ;
;
当点P′落在y轴上,如图3,
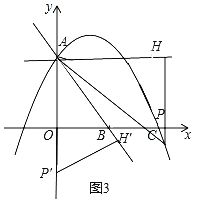
同理可得![]() =PH=
=PH=![]() m2﹣
m2﹣![]() m,
m,![]() =AH=m,
=AH=m,![]() =∠PHA=90°,
=∠PHA=90°,
∵![]() =∠BAO,
=∠BAO,
∴![]() ∽△AOB,
∽△AOB,
∴![]() :OB=AH′:AO,即(
:OB=AH′:AO,即(![]() m2﹣
m2﹣![]() m):3=m:4,
m):3=m:4,
整理得4m2﹣25m=0,
解得m1=![]() ,m2=0(舍去),
,m2=0(舍去),
此时P点横坐标为![]() ;
;
综上所述,P点横坐标为2![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3,则点B′的坐标为( )
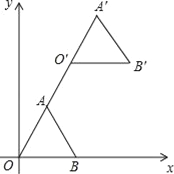
A. (4,2![]() ) B. (3,3
) B. (3,3![]() ) C. (4,3
) C. (4,3![]() ) D. (3,2
) D. (3,2![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( )
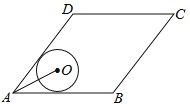
A.5 B.6 C.2![]() D.3
D.3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”期间,老张在某商场购物后,参加了出口处的抽奖活动.抽奖规则如下:每张发票可摸球一次,每次从装有大小形状都相同的1个白球和2个红球的盒子中,随机摸出一个球,若摸出的是白球,则获得一份奖品;若摸出的是红球,则不获奖.
(1)求每次摸球中奖的概率;
(2)老张想“我手中有两张发票,那么中奖的概率就翻了一倍.”你认为老张的想法正确吗?用列表法或画树形图分析说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,AC是半圆内一条弦,点D是![]() 的中点,DB交AC于点G,过点A作半圆的切线与BD的延长线交于点M,连接AD.点E是AB上的一动点,DE与AC相交于点F.
的中点,DB交AC于点G,过点A作半圆的切线与BD的延长线交于点M,连接AD.点E是AB上的一动点,DE与AC相交于点F.
(1)求证:MD=GD;
(2)填空:①当∠DEA= 时,AF=FG;
②若∠ABD=30°,当∠DEA= 时,四边形DEBC是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
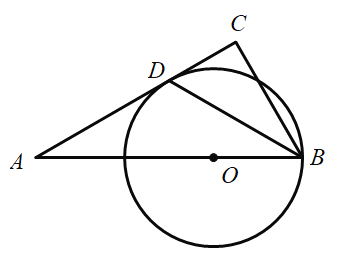
【题目】如图,在△ABC中,O是AB边上的点,以O为圆心,OB为半轻的⊙O与AC相切于点D,BD平分∠ABC,∠ABC=60°.
(1)求∠C的度数;
(2)若圆的半径OB=2,求线段CD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
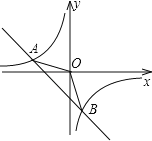
【题目】如图,已知A(﹣4,n),B(2,﹣4)是一次函数y=kx+b和反比例函数y=![]() 的图象的两个交点.
的图象的两个交点.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=100°,在同一平面内,将△ABC绕点A顺时针旋转到△AB1C1的位置,连接BB1,若BB1∥AC1,则∠CAC1的度数是( )

A.10°B.20°C.30°D.40°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com