
 如图,在△ABC中,∠ACB=90°,BC=AC=1,将△ABC绕点A顺时针旋转90°后得到△ADE,则BC边扫过部分图形(即阴影部分)的面积为$\frac{1}{4}$π(结果保留π).
如图,在△ABC中,∠ACB=90°,BC=AC=1,将△ABC绕点A顺时针旋转90°后得到△ADE,则BC边扫过部分图形(即阴影部分)的面积为$\frac{1}{4}$π(结果保留π). 分析 根据等腰直角三角形的性质得AB=$\sqrt{2}$AC=$\sqrt{2}$,再利用旋转的性质得∠BAD=∠CAE=90°,由于S扇形BAD+S△ADE=S△ABC+S扇形CAE+S阴影部分得S阴影部分=S扇形BAD-S扇形CAE,然后根据扇形的面积公式计算即可.
解答 解:∠ACB=90°,∵BC=AC=1,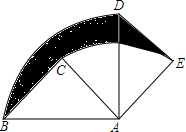
∴AB=$\sqrt{2}$AC=$\sqrt{2}$,
∵△ABC绕点A顺时针旋转90°后得到△ADE,
∴∠BAD=∠CAE=90°,
∵S扇形BAD+S△ADE=S△ABC+S扇形CAE+S阴影部分,
∴S阴影部分=S扇形BAD-S扇形CAE=$\frac{90•π•(\sqrt{2})^{2}}{360}$-$\frac{90•π•{1}^{2}}{360}$=$\frac{1}{4}$π.
故答案为$\frac{1}{4}$π.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.本题的关键是利用面积的和差计算不规则得几何图形的面积.


 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:解答题
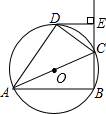 如图.四边形ABCD内接于⊙O,AC是⊙O的直径,DE⊥BC于E,CD平分∠ACE.
如图.四边形ABCD内接于⊙O,AC是⊙O的直径,DE⊥BC于E,CD平分∠ACE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
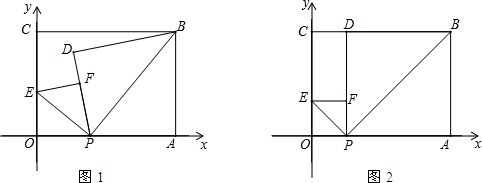
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
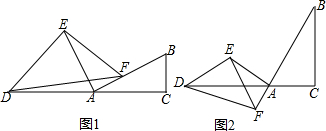
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com