
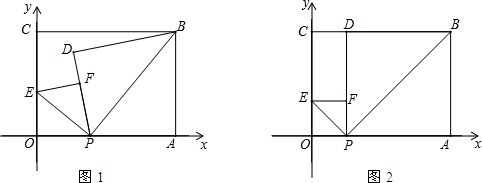
���� ��1������֪�ɵ�OP=x��OE=y����PA=4-x��AB=3�����û����ϵ��֤Rt��POE��Rt��BPA�������Ʊȿɵ�y����x�ĺ�����ϵʽ��
��2����ʱ����PAB����POE��Ϊ����ֱ�������Σ�BD=BA=3��CD=4-3=1����P��1��0����E��0��1����B��4��3�������������߽���ʽ��һ��ʽ���ɣ�
��3����PEΪֱ�DZߣ����P������Ϊֱ�Ƕ��㣬��ʱ��EPB=90�㣬B����ϣ���EҲ������Ϊֱ�Ƕ��㣬���ý�ֱ��PB����ƽ�ƹ�E��ķ�����ȷ����ʱ��ֱ��EQ����ʽ�����������߽���ʽ�����������Q���꣮
��� �⣺��1�����⣬AB=OC=m��OA=4����EOP=��PAB=90�㣬
��P��x��0����E��0��y����
��OP=x��OE=y��AP=4-x��
�߽���POE��PE���ۣ��õ���PFE��
���EPO+��APB=90�㣬
�֡ߡ�EPO+��OEP=90�㣬
���OEP=��APB��
���OEP�ס�APB��
��$\frac{EO}{PA}=\frac{OP}{AB}$��$\frac{y}{4-x}=\frac{x}{m}$��
��$y=\frac{x��4-x��}{m}=\frac{{-{x^2}+4x}}{m}$��
��$y=\frac{{-{{��x-2��}^2}+4}}{m}$��
��x=2ʱ��yȡ�����ֵ$y=\frac{4}{m}$��
��2������B��4��3��������PAB��PB���ۣ��õ���PDB������POE��PE���ۣ��õ���PFE��
���PBA=$\frac{1}{2}$��ABC=45�㣬��OPE=$\frac{1}{2}��$OPF��
�ߡ�COA=��ABC=90�㣬
���BAP�͡�EOPΪ����ֱ�������Σ�
��PA=AB=3��
��OP=1��
��OE=OP=1��
��P��1��0����E��0��1����
������B��P��E��������Ϊy=ax2+bx+1��
�߹��㣨4��3���ͣ�1��0����
��$\left\{\begin{array}{l}{0=a+b+1}\\{3=16a+4b+1}\end{array}\right.$
���a=$\frac{1}{2}$��b=-$\frac{3}{2}$��
���E��P��B����������ߵĽ���ʽΪ��$y=\frac{1}{2}{x^2}-\frac{3}{2}x+1$��
��3�������֪��EPB=90�㣬
��Q1��4��3���������⣬
��EQ2��BP��BP��y=x-1��
��EQ2��y=x+1��
��������$y=\frac{1}{2}{x^2}-\frac{3}{2}x+1$��
�ⷽ����$\left\{\begin{array}{l}{y=x+1}\\{y=\frac{1}{2}{x}^{2}-\frac{3}{2}x+1}\end{array}\right.$��$\left\{\begin{array}{l}{{x}_{1}=5}\\{{y}_{1}=6}\end{array}\right.$��$\left\{\begin{array}{l}{{x}_{2}=0}\\{{y}_{2}=1}\end{array}\right.$��
��Q2��5��6����
���ϣ�Q��������ǣ�4��3����5��6����
���� ���⿼�������������ε��ж������ʣ�����֤�����Ƶķ��������Զ�Ӧ����ȵ������������ƣ����Զ�Ӧ�߶�Ӧ�ɱ����Ҽн���ȵ������������ƣ����߶�Ӧ�ɱ����������������ƣ�����ϵ�����IJ��裺�������������ʽ������֪����������õ�һ�������飬���������Ľ⼴�ɵõ�������ĸ��ֵ��ȷ������������ʽ��ͬʱע�ⷭ�۵õ�������ȫ���Լ����շ������۵���ѧ˼�룮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
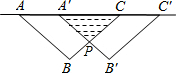 ��ͼ���ѵ���Rt��ABC��AC����ƽ�Ƶ�����Rt��A��B��C���λ��ʱ�������ص��IJ��ֵ������Rt��ABC�����$\frac{1}{4}$����AB=$\sqrt{2}$cm�������ƶ��ľ���AA��=1cm��
��ͼ���ѵ���Rt��ABC��AC����ƽ�Ƶ�����Rt��A��B��C���λ��ʱ�������ص��IJ��ֵ������Rt��ABC�����$\frac{1}{4}$����AB=$\sqrt{2}$cm�������ƶ��ľ���AA��=1cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 12 | B�� | 24 | C�� | 36 | D�� | 12$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У���ACB=90�㣬BC=AC=1������ABC�Ƶ�A˳ʱ����ת90���õ���ADE����BC��ɨ������ͼ�Σ�����Ӱ���֣������Ϊ$\frac{1}{4}$�У���������У���
��ͼ���ڡ�ABC�У���ACB=90�㣬BC=AC=1������ABC�Ƶ�A˳ʱ����ת90���õ���ADE����BC��ɨ������ͼ�Σ�����Ӱ���֣������Ϊ$\frac{1}{4}$�У���������У����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 С����¥���Ͽ�������ɽ����һ�������������еIJ������ϣ���������Ƥ�ߣ���������������յ�֪ʶ��ѡ��ǡ��������������ߣ�����ȷ��1��
С����¥���Ͽ�������ɽ����һ�������������еIJ������ϣ���������Ƥ�ߣ���������������յ�֪ʶ��ѡ��ǡ��������������ߣ�����ȷ��1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
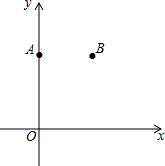 ��ͼ����ƽ��ֱ������ϵxOy�У���A��0��8������B��6��8����
��ͼ����ƽ��ֱ������ϵxOy�У���A��0��8������B��6��8�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
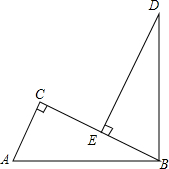 ��ͼ����ABD=90�㣬AB=BD��AC��BC��DE��BC������ֱ�ΪC��E����֤��AC+CE=DE��
��ͼ����ABD=90�㣬AB=BD��AC��BC��DE��BC������ֱ�ΪC��E����֤��AC+CE=DE���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com