
【题目】如图,BD是⊙O的直径, A、C是⊙O上的两点,且AB=AC,AD与BC的延长线交于点E.
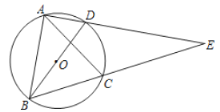
(1)求证:△ABD∽△AEB;
(2)若AD=1,DE=3,求BD的长.
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接DG,过点A作AH∥DG,交BG于点H.连接HF,AF,其中AF交EC于点M.
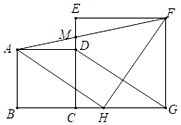
(1)求证:△AHF为等腰直角三角形.
(2)若AB=3,EC=5,求EM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂计划生产A、B两种产品共100件,已知A产品每件可获利润400元,B产品每件可获利润500元,其中规定生产B产品的数量不超过A产品数量的2倍,设生产A产品的数量为x(件),生产两种产品的获利总额为y(元)
(1)写出y与x之间的函数表达式;
(2)该厂生产A、B两种产品各多少台,才能使获利总额最大?最大利润是多少?
(3)在实际生产过程中,A产品生产成本下降了m(0<m<200)元且最多生产60件,B产品生产成本不变,请根据以上信息,设计出该厂生产100件A、B两种产品获利最多的生产方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(![]() )和B(4,6),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,6),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
(1)求抛物线的解析式;
(2)当C为抛物线顶点的时候,求![]() 的面积.
的面积.
(3)是否存在质疑的点P,使![]() 的面积有最大值,若存在,求出这个最大值,若不存在,请说明理由.
的面积有最大值,若存在,求出这个最大值,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
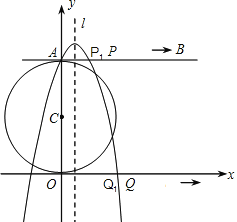
【题目】如图,在平面直角坐标系中,以点C(0,4)为圆心,半径为4的圆交y轴正半轴于点A,AB是⊙C的切线.动点P从点A开始沿AB方向以每秒1个单位长度的速度运动,点Q从O点开始沿x轴正方向以每秒4个单位长度的速度运动,且动点P、Q从点A和点O同时出发,设运动时间为t(秒).
(1)当t=1时,得到P1、Q1,求经过A、P1、Q1三点的抛物线解析式及对称轴l;
(2)当t为何值时,直线PQ与⊙C相切?并写出此时点P和点Q的坐标;
(3)在(2)的条件下,抛物线对称轴l上存在一点N,使NP+NQ最小,求出点N的坐标并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() (
(![]() 为常数,
为常数,![]() )经过点
)经过点![]() ,且关于直线
,且关于直线![]() 对称,
对称,![]() 是抛物线与x轴的一个交点.有下列结论:①方程
是抛物线与x轴的一个交点.有下列结论:①方程![]() 的一个根是x=-2;②若
的一个根是x=-2;②若![]() ,则
,则![]() ;③若
;③若![]() 时,方程
时,方程![]() 有两个相等的实数根,则
有两个相等的实数根,则![]() ;④若
;④若![]() 时,
时,![]() ,则
,则![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() (b,c为常数)与x轴交于点
(b,c为常数)与x轴交于点![]() 和
和![]() ,与y轴交于点A,点E为抛物线顶点。
,与y轴交于点A,点E为抛物线顶点。
(Ⅰ)当![]() 时,求点A,点E的坐标;
时,求点A,点E的坐标;
(Ⅱ)若顶点E在直线![]() 上,当点A位置最高时,求抛物线的解析式;
上,当点A位置最高时,求抛物线的解析式;
(Ⅲ)若![]() ,当
,当![]() 满足
满足![]() 值最小时,求b的值。
值最小时,求b的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
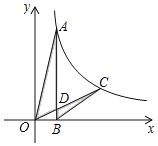
【题目】如图,已知点A,点C在反比例函数y=![]() (k>0,x>0)的图象上,AB⊥x轴于点B,OC交AB于点D,若CD=OD,则△AOD与△BCD的面积比为__.
(k>0,x>0)的图象上,AB⊥x轴于点B,OC交AB于点D,若CD=OD,则△AOD与△BCD的面积比为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某企业承接了上海世博会的礼品盒制作业务,他们购得规格是170cm×40cm的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下A型与B型两种板材.如图1所示,(单位:cm)
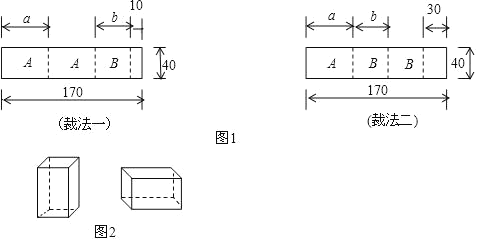
(1)列出方程(组),求出图甲中a与b的值.
(2)若将30张标准板材用裁法一裁剪,4张标准板材用裁法二裁剪,再将得到的A型与B型板材做侧面和底面,做成图2的竖式与横式两种无盖礼品盒.
①两种裁法共产生A型板材 张,B型板材 张;
②做成的竖式和横式两种无盖礼品盒总数最多是多少个?此时横式无盖礼品盒可以做多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com