计算$\frac{1}{1+\root{4}{10}}+\frac{1}{1-\root{4}{10}}+\frac{2}{1+\sqrt{10}}$的值．题目和参考答案——青夏教育精英家教网—

15．计算$\frac{1}{1+\root{4}{10}}+\frac{1}{1-\root{4}{10}}+\frac{2}{1+\sqrt{10}}$的值．

分析直接利用平方差公式化简各式，进而求出答案．

解答解：原式=$\frac{1-\root{4}{10}}{（1+\root{4}{10}）（1-\root{4}{10}）}$+$\frac{1+\root{4}{10}}{（1-\root{4}{10}）（1+\root{4}{10}）}$+$\frac{2（1-\sqrt{10}）}{（1+\sqrt{10}）（1-\sqrt{10}）}$
=$\frac{2}{1-\sqrt{10}}$+$\frac{2（1-\sqrt{10}）}{（1+\sqrt{10}）（1-\sqrt{10}）}$
=$\frac{2（1+\sqrt{10}）}{（1-\sqrt{10}）（1+\sqrt{10}）}$+$\frac{2（1-\sqrt{10}）}{（1+\sqrt{10}）（1-\sqrt{10}）}$
=-$\frac{4}{9}$．

点评此题主要考查了实数运算，正确应用平方差公式是解题关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：选择题

5．

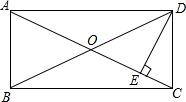如图，在矩形ABCD中，DE⊥AC于E，∠EDC：∠EDA=1：3，且DE=2$\sqrt{2}$，则AC的长是（　　）

A．

B．

C．

4$\sqrt{2}$

D．

8$\sqrt{2}$

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

6．

如图，AD是△ABC的中线，E、F分别是AB、AC的中点，求证：四边形AEDF是平行四边形．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

3．

如图，在四边形ABCD中，AE⊥BD，CF⊥BD，且AE=CF，∠BAC=∠DCA．求证：四边形ABCD是平行四边形．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

10．抛物线y=ax²+bx+c与x轴交于A，B两点，与y轴交于点C（0，4），且点B的坐标为（-4，0），点A在原点和点B之间，则a的取值范围是a＞$\frac{1}{4}$．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

2．

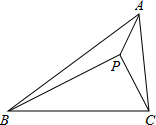如图，△ABC中，∠BAC=60°，AB=2AC，点P在△ABC内，且PA=$\sqrt{3}$，PB=5，PC=2，则△ABC的面积为（　　）

A．

3+$\frac{7}{2}$$\sqrt{3}$

B．

3+$\frac{5}{2}$$\sqrt{3}$

C．

3+$\sqrt{3}$

D．

3+$\frac{1}{2}$$\sqrt{3}$

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

9．

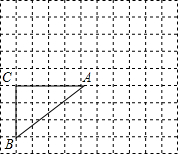下列网格图中，每个小正方形边长均为1个单位，在Rt△ABC中，AC=4，BC=3，∠C=90°．若点B的坐标为（-3，-3），试在图中画出平面直角坐标系，根据所建立的坐标系，在给出的网格中作出与△ABC位似的△A₁B₁C₁，使得位似中心为原点，△A₁B₁C₁与△ABC的相似比是2，并写出A₁、B₁、C₁点的坐标．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

6．

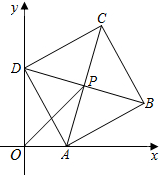已知：如图，平面直角坐标系xOy中，正方形ABCD的边长为4，它的顶点A在x轴的正半轴上运动（点A，D都不与原点重合），顶点B，C都在第一象限，且对角线AC，BD相交于点P，连接OP．设点P到y轴的距离为d，则在点A，D运动的过程中，d的取值范围是2＜d≤2$\sqrt{2}$．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

7．将直线y=2x-5向上平移7个单位所得的直线的解折式为y=2x+2．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学