
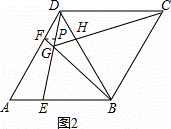
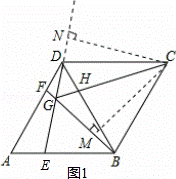
如图,在菱形ABCD中,AB=BD,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.给出如下几个结论:
①△AED≌△DFB;②S四边形BCDG=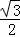 CG2;③若AF=2DF,则BG=6GF;④CG与BD一定不垂直;⑤∠BGE的大小为定值.
CG2;③若AF=2DF,则BG=6GF;④CG与BD一定不垂直;⑤∠BGE的大小为定值.
其中正确的结论个数为( )
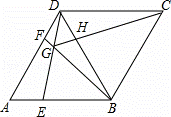
A.4 B. 3 C. 2 D. 1
B 解:①∵ABCD为菱形,∴AB=AD,
∵AB=BD,∴△ABD为等边三角形,
∴∠A=∠BDF=60°,
又∵AE=DF,AD=BD,
∴△AED≌△DFB,故本选项正确;
②∵∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°=∠BCD,
即∠BGD+∠BCD=180°,
∴点B、C、D、G四点共圆,
∴∠BGC=∠BDC=60°,∠DGC=∠DBC=60°,
∴∠BGC=∠DGC=60°,
过点C作CM⊥GB于M,CN⊥GD于N(如图1),
则△CBM≌△CDN(AAS),
∴S四边形BCDG=S四边形CMGN,
S四边形CMGN=2S△CMG,
∵∠CGM=60°,
∴GM=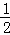 CG,CM=
CG,CM=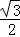 CG,
CG,
∴S四边形CMGN=2S△CMG=2×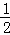 ×
×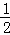 CG×
CG×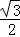 CG=
CG=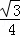 CG2,故本选项错误;
CG2,故本选项错误;
③过点F作FP∥AE于P点(如图2),
∵AF=2FD,
∴FP:AE=DF:DA=1:3,
∵AE=DF,AB=AD,
∴BE=2AE,
∴FP:BE=FP: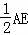 =1:6,
=1:6,
∵FP∥AE,
∴PF∥BE,
∴FG:BG=FP:BE=1:6,
即BG=6GF,故本选项正确;
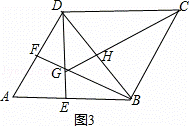
④当点E,F分别是AB,AD中点时(如图3),
由(1)知,△ABD,△BDC为等边三角形,
∵点E,F分别是AB,AD中点,
∴∠BDE=∠DBG=30°,
∴DG=BG,
在△GDC与△BGC中,
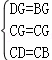 ,
,
∴△GDC≌△BGC,
∴∠DCG=∠BCG,
∴CH⊥BD,即CG⊥BD,故本选项错误;
⑤∵∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°,为定值,
故本选项正确;
综上所述,正确的结论有①③⑤,共3个,
故选B.


科目:初中数学 来源: 题型:
如图,已知D为△ABC边AB的中点,E在AC上,将△ABC沿着DE折叠,使A点落在BC上的F处.若∠B=65°,则∠BDF等于( )
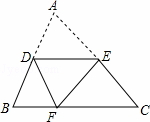
A. 65° B. 50° C. 60° D. 57.5°
查看答案和解析>>
科目:初中数学 来源: 题型:
某商场有A,B两种商品,若买2件A商品和1件B商品,共需80元;若买3件A商品和2件B商品,共需135元.
(1)设A,B两种商品每件售价分别为a元、b元,求a、b的值;
(2)B商品每件的成本是20元,根据市场调查:若按(1)中求出的单价销售,该商场每天销售B商品100件;若销售单价每上涨1元,B商品每天的销售量就减少5件.
①求每天B商品的销售利润y(元)与销售单价(x)元之间的函数关系?
②求销售单价为多少元时,B商品每天的销售利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
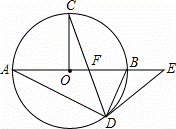
如图,在⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,在AB的延长线上有点E,且EF=ED.
(1)求证:DE是⊙O的切线;
(2)若OF:OB=1:3,⊙O的半径R=3,求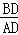 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,由一些完全相同的小正方体搭成的几何体的俯视图和左视图,组成这个几何体的小正方体的个数是( )
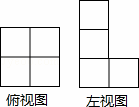
A. 5或6或7 B. 6或7 C. 6或7或8 D. 7或8或9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com