
如图,在边长为2的等边△ABC中,D为BC的中点,E是AC边上一点,则BE+DE的最小值为 .
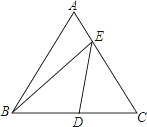
科目:初中数学 来源: 题型:
某电器商场销售A,B两种型号计算器,两种计算器的进货价格分别为每台30元,40元. 商场销售5 台A型号和1台B型号计算器,可获利润76元;销售6台A型号和3台B型号计算器,可获利润 120元.
(1) 求商场销售A,B两种型号计算器的销售价格分别是多少元?(利润=销售价格﹣进货价格)
(2) 商场准备用不多于2500元的资金购进A,B两种型号计算器共70台,问最少需要购进A型号的 计算器多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
已知空气的单位体积质量是0.001239g/cm3,则用科学记数法表示该数为( )
A.1.239×10﹣3g/cm3 B. 1.239×10﹣2g/cm3
C.0.1239×10﹣2g/cm3 D. 12.39×10﹣4g/cm3
查看答案和解析>>
科目:初中数学 来源: 题型:
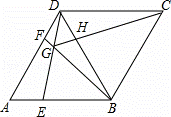
如图,在菱形ABCD中,AB=BD,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.给出如下几个结论:
①△AED≌△DFB;②S四边形BCDG=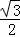 CG2;③若AF=2DF,则BG=6GF;④CG与BD一定不垂直;⑤∠BGE的大小为定值.
CG2;③若AF=2DF,则BG=6GF;④CG与BD一定不垂直;⑤∠BGE的大小为定值.
其中正确的结论个数为( )
A.4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
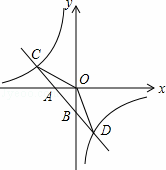
如图,已知一次函数y1=k1x+b的图象与x轴、y轴分别交于A、B两点,与反比例函数y2=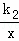 的图象分别交于C、D两点,点D(2,﹣3),点B是线段AD的中点.
的图象分别交于C、D两点,点D(2,﹣3),点B是线段AD的中点.
(1)求一次函数y1=k1x+b与反比例函数y2=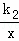 的解析式;
的解析式;
(2)求△COD的面积;
(3)直接写出y1>y2时自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
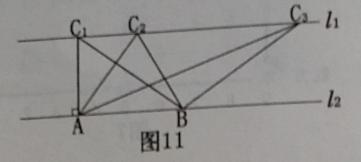
如图11,已知, l1∥l2,C1在l1上,并且C1A⊥l2,A为垂足,C2,C3是l1上任意两点,点B在l2上,设△ABC1的面积为S1,△ABC2的面积为S2,△ABC3的面积为S3,小颖认为S1=S2=S3,请帮小颖说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
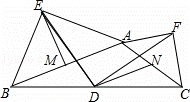
如图,在钝角△ABC中,分别以AB和AC为斜边向△ABC的外侧作等腰直角三角形ABE和等腰直角三角形ACF,EM平分∠AEB交AB于点M,取BC中点D,AC中点N,连接DN、DE、DF.下列结论:①EM=DN;②S△CDN=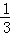 S四边形ABDN;③DE=DF;④DE⊥DF.其中正确的结论的个数是( )
S四边形ABDN;③DE=DF;④DE⊥DF.其中正确的结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com