练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如果成立，则a的取值范围是　　　　　　．


    　a≠　．

    【考点】分式的基本性质．

    【分析】根据分式的分子分母都乘以（或除以）同一个不为零的整式，分式的值不变，可得答案．

    【解答】解：成立，得

    2a﹣1≠0．

    解得a≠，

    故答案为：．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    某校想了解学生每周的课外阅读时间情况，随机调查了部分学生，对学生每周的课外阅读时间x（单位：小时）进行分组整理，并绘制了如图所示的不完整的频数分布直方图和扇形统计图．

    根据图中提供的信息，解答下列问题：

    （1）补全频数分布直方图；

    （2）求扇形统计图中m的值和“E”组对应的圆心角度数；

    （3）请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某学校为了解本校学生课外阅读的情况，从全体学生中随机抽取了部分学生进行调查，并将调查结果绘制成统计表．已知该校全体学生人数为1200人，由此可以估计每周课外阅读时间在1～2（不含1）小时的学生有　　　　　　人．　　

    每周课外阅读时间（小时）

    0～1

    1～2

    （不含1）

    2～3

    （不含2）

    超过3

    人  数

    7

    10

    14

    19

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     “低碳环保，你我同行”．两年来，扬州市区的公共自行车给市民出行带来切实方便．电视台记者在某区街头随机选取了市民进行调查，调查的问题是“您大概多久使用一次公共自行车？”，将本次调查结果归为四种情况：A．每天都用；B．经常使用；C．偶尔使用；D．从未使用．将这次调查情况整理并绘制如下两幅统计图如图2：

    根据图中的信息，解答下列问题：

    （1）本次活动共有　　　　　　位市民参与调查；

    （2）补全条形统计图和扇形统计图；

    （3）扇形统计图中A项所对应的圆心角的度数为　　　　　　

    （4）根据统计结果，若该区有46万市民，请估算每天都用公共自行车的市民约有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某学习小组设计了一个摸球试验，在袋中装有黑，白两种颜色的球，这些球的形状大小质地等完全相同，即除颜色外无其他差别．在看不到球的情况下，随机从袋中摸出一个球，记下颜色，再把它放回，不断重复．下表是由试验得到的一组统计数据：

    摸球的次数

    100

    200

    300

    400

    500

    600

    摸到白球的次数

    58

    118

    189

    237

    302

    359

    摸到白球的频率

    0.58

    0.59

    0.63

    0.593

    0.604

    0.598

    从这个袋中随机摸出一个球，是白球的概率约为　　　　　　．（结果精确到0.1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，点A是直线l外一点，在l上取两点B、C，分别以A、C为圆心，BC、AB长为半径画弧，两弧交于点D，分别连接AB、AD、CD，则四边形ABCD一定是（　　）

    A．平行四边形     B．矩形  C．菱形 D．梯形

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    实验室里，水平桌面上有甲、乙两个圆柱形容器（容器足够高），底面半径之比为1∶2，用一个管子在甲、乙两个容器的15厘米高度处连通（即管子底端离容器底15厘米）．已知只有乙容器中有水，水位高2厘米，如图所示．现同时向甲、乙两个容器注水，平均每分钟注入乙容器的水量是注入甲容器水量的k倍．开始注水1分钟，甲容器的水位上升a厘米，且比乙容器的水位低1厘米．其中a，k均为正整数，当甲、乙两个容器的水位都到达连通管子的位置时，停止注水．甲容器的水位有2次比

    乙容器的水位高1厘米，设注水时间为t分钟．

       （1）求k的值（用含a的代数式表示）．

       （2）当甲容器的水位第一次比乙容器的水位高1厘米时，求t的值．

    （3）当甲容器的水位第二次比乙容器的水位高1厘米时，求a，k，t的值．

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在△ABC中，BD平分∠ABC，BC的垂直平分线交BC于点E，交BD于点F，连结CF．若∠A=60°，∠ACF =45°，则∠ABC的度数为（    ）

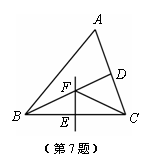    　   A．45°                  B．50°                        C．55°                        D．60°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，已知AB∥CD，BE平分∠ABC，DE平分∠ADC，∠BAD＝80°，试求：

        (1)∠EDC的度数；

    (2)若∠BCD＝n°，试求∠BED的度数．

     

     

     

     

     

     

    查看答案和解析>>

    同步练习册答案