
 如图1,点E为正方形ABCD的边AB上一点,EF⊥EC,且EF=EC,连接AF.
如图1,点E为正方形ABCD的边AB上一点,EF⊥EC,且EF=EC,连接AF.分析 (1)首先在BC上截取BG=BE,连接EG,求出∠BGE=45°,即可求出∠CGE=135°;然后根据全等三角形判定的方法,判断出△AEF≌△GCE,即可求出∠EAF的度数.
(2)①首先延长AF、CD交于点H,判断出∠FAD=45°,进而判断出四边形ABDH是平行四边形,推得DH=AB=CD,即可推得DM是△CFH的中位线,所以FH=2DM;然后在等腰直角三角形HAD中,根据AH=$\sqrt{2}$AD,可推得$\sqrt{2}$AD=AF+2DM.
②首先根据AF=10$\sqrt{2}$,AN=12,$\sqrt{2}$AD=AF+2MD,可得$\sqrt{2}$(12+DN)=10$\sqrt{2}$+2MD;然后根据AF∥DM,判断出△AFN∽△DMN,即可判断出$\frac{AN}{DN}=\frac{AF}{DM}$,据此推得DN、MD的关系,求出MD的长为多少即可.
解答 (1)解:如图1,在BC上截取BG=BE,连接EG,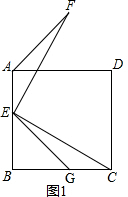 ,
,
∵BG=BE,∠EBG=90°,
∴∠BGE=45°,∠CGE=135°,
∵AB=BC,BG=BE,
∴AE=GC,
∵EF⊥EC,
∴∠AEF+∠BEC=90°,
∵∠GCE+∠BEC=90°,
∴∠AEF=∠GCE,
在△AEF和△GCE中,
$\left\{\begin{array}{l}{AE=GC}\\{∠AEF=∠GCE}\\{EF=EC}\end{array}\right.$,
∴△AEF≌△GCE,
∴∠EAF=∠CGE=135°,
即∠EAF的度数是135°.
(2)①证明:如图2,延长AF、CD交于点H,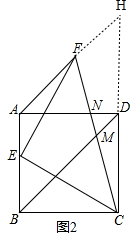 ,
,
由(1)知,∠EAF=135°,
∴∠FAD=135°-90°=45°,
∵∠ADB=45°,
∴AH∥BD,
又∵AB∥HD,
∴四边形ABDH是平行四边形,
∴DH=AB=CD,
即D是CH的中点,
∴DM是△CFH的中位线,
∴FH=2DM,
在等腰直角三角形HAD中,
AH=$\sqrt{2}$AD,
∵AH=AF+FH=AF+2DM,
∴$\sqrt{2}$AD=AF+2DM.
②解:如图3,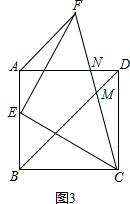 ,
,
∵AF=10$\sqrt{2}$,AN=12,$\sqrt{2}$AD=AF+2MD,
∴$\sqrt{2}$(12+DN)=10$\sqrt{2}$+2MD,
∵AF∥DM,
∴△AFN∽△DMN,
∴$\frac{AN}{DN}=\frac{AF}{DM}$,
即$\frac{12}{DN}=\frac{10\sqrt{2}}{DM}$,
∴DN=$\frac{3\sqrt{2}}{5}$MD,
把DN=$\frac{3\sqrt{2}}{5}$MD代入$\sqrt{2}$(12+DN)=10$\sqrt{2}$+2MD,
整理,可得
$\frac{6}{5}MD$+12$\sqrt{2}$=2MD+10$\sqrt{2}$,
解得MD=$\frac{5\sqrt{2}}{2}$,
即MD的长为$\frac{5\sqrt{2}}{2}$.
故答案为:$\frac{5\sqrt{2}}{2}$.
点评 (1)此题主要考查了四边形综合题,考查了分析推理能力,考查了数形结合思想的应用,要熟练掌握.
(2)此题还考查了全等三角形的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:①判定定理1:SSS--三条边分别对应相等的两个三角形全等.②判定定理2:SAS--两边及其夹角分别对应相等的两个三角形全等.③判定定理3:ASA--两角及其夹边分别对应相等的两个三角形全等.④判定定理4:AAS--两角及其中一个角的对边对应相等的两个三角形全等.⑤判定定理5:HL--斜边与直角边对应相等的两个直角三角形全等.
(3)此题还考查了三角形相似的判定和性质的应用,以及正方形的性质和应用,要熟练掌握.


科目:初中数学 来源: 题型:解答题
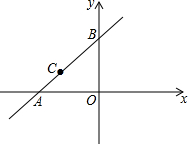 如图,直线y=x+4与坐标轴交于点A、B,点C(-3,m)在直线AB上,在y轴上找一点P,使PA+PC的值最小,求这个最小值及点P的坐标.
如图,直线y=x+4与坐标轴交于点A、B,点C(-3,m)在直线AB上,在y轴上找一点P,使PA+PC的值最小,求这个最小值及点P的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
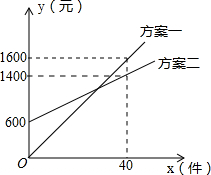 某销售公司推销一种产品,设x(种)是推销产品的数量,y(元)是付给推销员的月报酬.公司付给推销员的月报酬的两种方案如图所示,推销员可以任选一种与公司签订合同,看图解答下列问题:
某销售公司推销一种产品,设x(种)是推销产品的数量,y(元)是付给推销员的月报酬.公司付给推销员的月报酬的两种方案如图所示,推销员可以任选一种与公司签订合同,看图解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
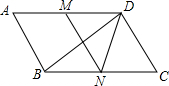 如图,在?ABCD中,∠C=60°,M、N分别是AD、BC的中点,BC=2CD
如图,在?ABCD中,∠C=60°,M、N分别是AD、BC的中点,BC=2CD查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com