
分析 首先两边同时减去$\frac{2}{x+2}$,然后去分母、去括号、移项、合并同类项、系数化成1即可求解.
解答 解:原式即$\frac{x+1}{2}$+$\frac{x-1}{3}$>1,
去分母,得:3(x+1)+2(x-1)>6,
去括号,得:3x+3+2x-2>6,
移项、合并同类项,得5x>5,
系数化成1得x>1.
x+2≠0,解得:x≠-2.
故不等式的解集是:x>1.
点评 本题考查了解简单不等式的能力,解答这类题学生往往在解题时不注意移项要改变符号这一点而出错.
解不等式要依据不等式的基本性质:
(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
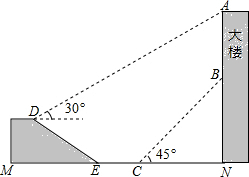 如图,大楼AN上悬挂一条幅AB,小颖在坡面D处测得条幅顶部A的仰角为30°,沿坡面向下走到坡脚E处,然后向大楼方向继续行走10米来到C处,测得条幅的底部B的仰角为45°,此时小颖距大楼底端N处20米.已知坡面DE=20米,山坡的坡度i=1:$\sqrt{3}$(即tan∠DEM=1:$\sqrt{3}$),且D、M、E、C、N、B、A在同一平面内,E、C、N在同一条直线上,求条幅的长度(结果精确到1米)(参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)
如图,大楼AN上悬挂一条幅AB,小颖在坡面D处测得条幅顶部A的仰角为30°,沿坡面向下走到坡脚E处,然后向大楼方向继续行走10米来到C处,测得条幅的底部B的仰角为45°,此时小颖距大楼底端N处20米.已知坡面DE=20米,山坡的坡度i=1:$\sqrt{3}$(即tan∠DEM=1:$\sqrt{3}$),且D、M、E、C、N、B、A在同一平面内,E、C、N在同一条直线上,求条幅的长度(结果精确到1米)(参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图1,点E为正方形ABCD的边AB上一点,EF⊥EC,且EF=EC,连接AF.
如图1,点E为正方形ABCD的边AB上一点,EF⊥EC,且EF=EC,连接AF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
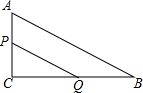 如图,Rt△ACB中,∠ACB=90°,AC=4,BC=10.点P、Q分别是两直角边CA、CB上的动点,点P以1个单位长度/秒的速度从点C运动向点A运动,点Q以2个单位长度/秒的速度从点C运动向点B即运动,当点P运动到点A时,两点均停止运动.设四边形APQB的面积为S,则S关于t的函数的图象大致是( )
如图,Rt△ACB中,∠ACB=90°,AC=4,BC=10.点P、Q分别是两直角边CA、CB上的动点,点P以1个单位长度/秒的速度从点C运动向点A运动,点Q以2个单位长度/秒的速度从点C运动向点B即运动,当点P运动到点A时,两点均停止运动.设四边形APQB的面积为S,则S关于t的函数的图象大致是( )| A. | 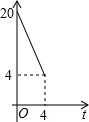 | B. | 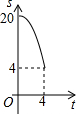 | C. | 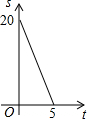 | D. | 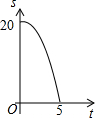 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
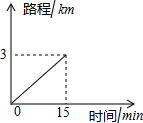 小丽家离学校2km,步行到校需30min,小丽的同学小军上学要经过小丽家,小军骑车上学行驶的路程与时间的关系如图所示.
小丽家离学校2km,步行到校需30min,小丽的同学小军上学要经过小丽家,小军骑车上学行驶的路程与时间的关系如图所示. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com