
分析 (1)先算乘法,合并同类项,算除法,最后代入求出即可;
(2)根据完全平方公式变形,再代入求出即可;
(3)先根据多项式乘以多项式法则算乘法,合并同类项,根据已知得出方程,求出p、q即可.
解答 解:(1)[(2x-3y)2-2x(2x+3y)]÷9y
=[4x2-12xy+9y2-4x2-6xy]÷9y
=(-18xy+9y2)÷9y
=-3x+y,
当x=3,y=-2时,原式=-3×3+(-2)=-11;
(2)∵a+b=4,ab=3,
∴(a-b)2
=(a+b)2-4ab
=42-4×3
=4;
(3)(x2+px+8)(x2-3x+q)
=x4-3x3+qx2+px3-3px2+pqx+8x2-24x+8q
=x4+(-3+p)x3+(q-3p+8)x2+(pq-24)x+8q,
∵(x2+px+8)(x2-3x+q)的乘积中不含x2与x3的项,
∴-3+p=0,q-3p+8=0,
解得:p=3,q=1.
点评 本题考查了整式的混合运算和求值的应用,能根据所学的知识点进行化简是解此题的关键.


科目:初中数学 来源: 题型:解答题
 已知二次函数y=x2-2(k+1)x+k2-2k-3与x轴有两个交点.
已知二次函数y=x2-2(k+1)x+k2-2k-3与x轴有两个交点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
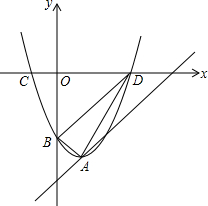 如图,抛物线y=x2-2x+c的顶点A在直线l:y=x-5上.
如图,抛物线y=x2-2x+c的顶点A在直线l:y=x-5上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知某几何体的三视图的侧视图是一个正三角形,如图所示,则该几何体的体积等于( )
已知某几何体的三视图的侧视图是一个正三角形,如图所示,则该几何体的体积等于( )| A. | 12$\sqrt{3}$ | B. | 16$\sqrt{3}$ | C. | 20$\sqrt{3}$ | D. | 32$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com