
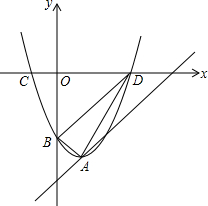
 如图,抛物线y=x2-2x+c的顶点A在直线l:y=x-5上.
如图,抛物线y=x2-2x+c的顶点A在直线l:y=x-5上.分析 (1)先根据抛物线的解析式得出其对称轴,由此得到顶点A的横坐标,然后代入直线l的解析式中即可求出点A的坐标,根据二次函数的解析式求得B,D两点的坐标,于是求出直线BD的解析式,根据两直线斜率相等,得到结论;
(2)由A点坐标可确定抛物线的解析式,进而可得到点B的坐标.则AB、AD、BD三边的长可得,然后根据边长确定三角形的形状.
(3)若以点P、A、B、D为顶点的四边形是平行四边形,应分①AB为对角线、②AD为对角线两种情况讨论,即①AD∥PB,AD=PB、②AB∥PD,AB=PD,然后结合勾股定理以及边长的等量关系列方程求出P点的坐标.
解答 解:(1)∵抛物线的对称轴是直线x=-$\frac{-2}{2}$=1,且顶点A在y=x-5上,
∴当x=1时,y=1-5=-4,
∴A(1,-4),
∴-4=12-2+c,
∴c=-3,
∴B(0,-3),
令y=0,即x2-2x-3=0,
∴x1=-1,x2=3,
∴D(3.0),
∴直线BD的解析式为:y=x-3,
∴BD∥直线l,
故答案为:x=1,(1,-4),(0,-3),平行;
(2)△ABD是直角三角形.
将A(1,-4)代入y=x2-2x+c,可得,1-2+c=-4,∴c=-3,
∴y=x2-2x-3,∴B(0,-3)
当y=0时,x2-2x-3=0,x1=-1,x2=3
∴C(-1,0),D(3,0),
BD2=OB2+OD2=18,AB2=(4-3)2+12=2,AD2=(3-1)2+42=20,
BD2+AB2=AD2,
∴∠ABD=90°,即△ABD是直角三角形.
(3)存在.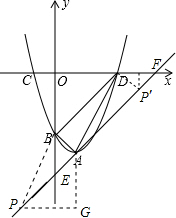
由题意知:直线y=x-5交y轴于点E(0,-5),交x轴于点F(5,0)
∴OE=OF=5,
又∵OB=OD=3
∴△OEF与△OBD都是等腰直角三角形
∴BD∥l,即PA∥BD
则构成平行四边形只能是PADB或PABD,如图,
过点P作y轴的垂线,过点A作x轴的垂线交过P且平行于x轴的直线于点G.
设P(x1,x1-5),则G(1,x1-5)
则PG=|1-x1|,AG=|5-x1-4|=|1-x1|
PA=BD=3$\sqrt{2}$,
由勾股定理得:
(1-x1)2+(1-x1)2=18,x12-2x1-8=0,x1=-2或4
∴P(-2,-7)或P(4,-1),
存在点P(-2,-7)或P(4,-1)使以点A、B、D、P为顶点的四边形是平行四边形.
点评 本题考查了二次函数解析式的确定、勾股定理、平行四边形的判定等基础知识,综合性较强;(3)题应注意分类讨论,以免漏解,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
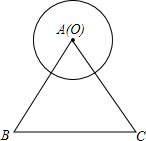 如图,正三角形ABC的边长为6$\sqrt{3}$,当圆心O从点A出发,沿着线路AB-BC-CA运动,最后回到点A,⊙O与△ABC任意一边都不会相切时,称为“零相切”;在运动过程中,当⊙O只与△ABC一边相切时,称为“单次相切”;在运动过程中,当⊙O与△ABC两边都相切时,成为继“双次相切”.
如图,正三角形ABC的边长为6$\sqrt{3}$,当圆心O从点A出发,沿着线路AB-BC-CA运动,最后回到点A,⊙O与△ABC任意一边都不会相切时,称为“零相切”;在运动过程中,当⊙O只与△ABC一边相切时,称为“单次相切”;在运动过程中,当⊙O与△ABC两边都相切时,成为继“双次相切”.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com