
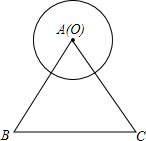
 如图,正三角形ABC的边长为6$\sqrt{3}$,当圆心O从点A出发,沿着线路AB-BC-CA运动,最后回到点A,⊙O与△ABC任意一边都不会相切时,称为“零相切”;在运动过程中,当⊙O只与△ABC一边相切时,称为“单次相切”;在运动过程中,当⊙O与△ABC两边都相切时,成为继“双次相切”.
如图,正三角形ABC的边长为6$\sqrt{3}$,当圆心O从点A出发,沿着线路AB-BC-CA运动,最后回到点A,⊙O与△ABC任意一边都不会相切时,称为“零相切”;在运动过程中,当⊙O只与△ABC一边相切时,称为“单次相切”;在运动过程中,当⊙O与△ABC两边都相切时,成为继“双次相切”.分析 (1)根据切线的性质可知,圆心到切线的距离等于半径,⊙O与△ABC首次“单次相切”时,与边AC相切,过点O向三角形的三边作垂线利用锐角三角函数可得AO;第二次相切时与边BC相切,同理可得O″B,可得OA;同理可得第二次与BC相切,与AB相切,可得4次;根据双相切定义可知⊙O到两边距离相等,即为三边的中点,可得OP,OP>r,可知无双相切;
(2)与(1)同理可得半径为9时,AO=6$\sqrt{3}$,可知当圆心在A,B,C上时⊙O与△ABC“单次相切”,所以可得共3次单相切;因为⊙O的半径不等于$\frac{9}{2}$,所以无双相切;
(3)由(1)(2)分析可得结论.
解答 解(1)如图1,过O′点作O′P′⊥AC,
在Rt△AO′P′中,∠A=60°,O′P′=$\sqrt{3}$,
∴AO=$\frac{O′P′}{sin∠A}$=$\frac{\sqrt{3}}{sin60°}$=2,
∴⊙O与△ABC首次“单次相切”时,OA的长为2;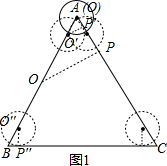
同理可得,O″B=$\frac{O″P″}{sin∠B}$=$\frac{\sqrt{3}}{sin60°}$=2,
∴OA=6$\sqrt{3}$-2,
∴⊙O与△ABC第二次“单次相切”时,OA的长为6$\sqrt{3}$-2;
同理可得,⊙O与△ABC“单次相切”的次数为4,
若双次相切则⊙O到两边距离相等,即为三边的中点,
此时,OP=$3\sqrt{3}•sin60°$=$\frac{9}{2}$,
∵$\sqrt{3}<\frac{9}{2}$,
∴不可能双次相切;
故答案为:2,6$\sqrt{3}-2$,4,不可能;
(2)如图2,AO′=$\frac{OP}{sin∠A}$=$\frac{9}{sin60°}$=6$\sqrt{3}$,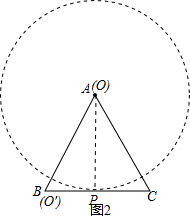
∴当圆心在A,B,C上时⊙O与△ABC“单次相切”,
∴⊙O与△ABC“单次相切”的次数为3,
由(1)得,
∵⊙O的半径不等于$\frac{9}{2}$,
∴不可能双次相切,
故答案为:3,不可能;
(3)依照(1)、(2)研究方法可得,当0<r<$\frac{9}{2}$时,.⊙O与△ABC有且仅有单相切4次;
当r=$\frac{9}{2}$时,有且仅有双相切3次;
当$\frac{9}{2}$<r≤9时,有且仅有单相切3次;
当r>9时,无相切.
点评 本题主要考查了切线的性质和三角函数,理解单相切与双相切的定义,数形结合是解答此题的关键.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
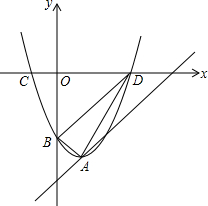 如图,抛物线y=x2-2x+c的顶点A在直线l:y=x-5上.
如图,抛物线y=x2-2x+c的顶点A在直线l:y=x-5上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知某几何体的三视图的侧视图是一个正三角形,如图所示,则该几何体的体积等于( )
已知某几何体的三视图的侧视图是一个正三角形,如图所示,则该几何体的体积等于( )| A. | 12$\sqrt{3}$ | B. | 16$\sqrt{3}$ | C. | 20$\sqrt{3}$ | D. | 32$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查某食品添加剂是否超标宜用普查 | |
| B. | 甲、乙两组的平均成绩相同,方差分别是S甲2=3.6,S乙2=3.0,则两组成绩一样稳定 | |
| C. | 同一年出生的367名学生中,至少有两人的生日是同一天是随机事件 | |
| D. | 调查10名运动员兴奋剂的使用情况适宜全面调查 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com