
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:解答题
 点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|. 利用数形结合思想回答下列问题:
点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|. 利用数形结合思想回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
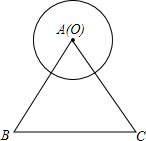 如图,正三角形ABC的边长为6$\sqrt{3}$,当圆心O从点A出发,沿着线路AB-BC-CA运动,最后回到点A,⊙O与△ABC任意一边都不会相切时,称为“零相切”;在运动过程中,当⊙O只与△ABC一边相切时,称为“单次相切”;在运动过程中,当⊙O与△ABC两边都相切时,成为继“双次相切”.
如图,正三角形ABC的边长为6$\sqrt{3}$,当圆心O从点A出发,沿着线路AB-BC-CA运动,最后回到点A,⊙O与△ABC任意一边都不会相切时,称为“零相切”;在运动过程中,当⊙O只与△ABC一边相切时,称为“单次相切”;在运动过程中,当⊙O与△ABC两边都相切时,成为继“双次相切”.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com