
分析 只需分别考虑被减数和减数的底数与积中的两个因素之间的关系,就可解决问题.
解答 解:39×41=402-12=($\frac{41+39}{2}$)2-($\frac{41-39}{2}$)2,
48×52=502-22=($\frac{52+48}{2}$)2-($\frac{52-48}{2}$)2,
52×62=572-52=($\frac{62+52}{2}$)2-($\frac{62-52}{2}$)2,
67×77=722-52=($\frac{77+67}{2}$)2-($\frac{77-67}{2}$)2,
…
由此可得:mn=${(\frac{n+m}{2})^2}-{(\frac{n-m}{2})^2}$.
故答案为${(\frac{n+m}{2})^2}-{(\frac{n-m}{2})^2}$.
点评 本题是规律探究题,主要考查了归纳探究的能力.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:解答题
 已知二次函数y=x2-2(k+1)x+k2-2k-3与x轴有两个交点.
已知二次函数y=x2-2(k+1)x+k2-2k-3与x轴有两个交点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
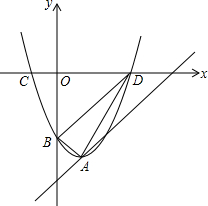 如图,抛物线y=x2-2x+c的顶点A在直线l:y=x-5上.
如图,抛物线y=x2-2x+c的顶点A在直线l:y=x-5上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知某几何体的三视图的侧视图是一个正三角形,如图所示,则该几何体的体积等于( )
已知某几何体的三视图的侧视图是一个正三角形,如图所示,则该几何体的体积等于( )| A. | 12$\sqrt{3}$ | B. | 16$\sqrt{3}$ | C. | 20$\sqrt{3}$ | D. | 32$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com