
分析 先根据分式混合运算的法则把原式进行化简,再求出x的值代入进行计算即可.
解答 解:原式=$\frac{x}{(x+1)(x-1)}$÷$\frac{x}{x-1}$
=$\frac{x}{(x+1)(x-1)}$•$\frac{x-1}{x}$
=$\frac{1}{x+1}$,
当x=2×$\frac{\sqrt{2}}{2}$-$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=$\sqrt{2}$-1时,原式=$\frac{1}{\sqrt{2}-1+1}$=$\frac{\sqrt{2}}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.


科目:初中数学 来源: 题型:填空题
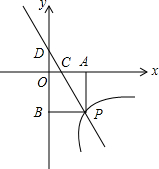 如图,一次函数y=kx+1的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点P,PA⊥x轴于点A,PB⊥y轴于点B,一次函数的图象分别交x轴,y轴于点C,点D.且
如图,一次函数y=kx+1的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点P,PA⊥x轴于点A,PB⊥y轴于点B,一次函数的图象分别交x轴,y轴于点C,点D.且查看答案和解析>>
科目:初中数学 来源: 题型:解答题
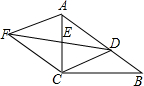 如图,在Rt△ABC中,∠ACB=90°,点D是边AB上一点(点D不与点A重合),点E是AC的中点,连结DE并延长至点F,使EF=DE,连结AF、CF.
如图,在Rt△ABC中,∠ACB=90°,点D是边AB上一点(点D不与点A重合),点E是AC的中点,连结DE并延长至点F,使EF=DE,连结AF、CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
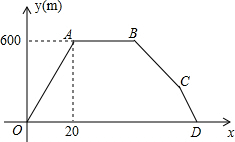 某山山脚的M处到山顶的N处有一条长为600米的登山路,小李沿此路从M走到N,停留后再原路返回,期间小李离开M处的路程y米与离开M处的时间x分(x>0)之间的函数关系如图中折线OABCD所示.
某山山脚的M处到山顶的N处有一条长为600米的登山路,小李沿此路从M走到N,停留后再原路返回,期间小李离开M处的路程y米与离开M处的时间x分(x>0)之间的函数关系如图中折线OABCD所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
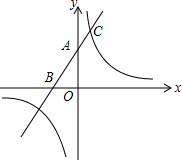 如图,在平面直角坐标系中,直线l:y1=2x+4,与y轴交于点A,与x轴交于点B,反比例函数y2=$\frac{k}{x}$与直线l交于点C,且AB=2AC.
如图,在平面直角坐标系中,直线l:y1=2x+4,与y轴交于点A,与x轴交于点B,反比例函数y2=$\frac{k}{x}$与直线l交于点C,且AB=2AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
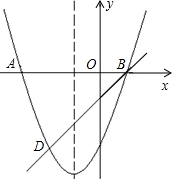 如图,二次函数y=x2+bx+c的图象与x轴交于A、B两点,且A点坐标为(-3,0),经过B点的直线交抛物线于点D(-2,-3).
如图,二次函数y=x2+bx+c的图象与x轴交于A、B两点,且A点坐标为(-3,0),经过B点的直线交抛物线于点D(-2,-3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.663×107 | B. | 663×104 | C. | 6.63×107 | D. | 6.63×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com