
分析 (1)根据待定系数法,可得函数解析式;
(2)根据图象向上平移加,可得新抛物线,根据自变量与函数值的对应关系,可得B、D点坐标,根据对称点的中点在对称轴的直线上,对称点的直线的一次项系数与对称轴的一次项的系数互为负倒数,可得方程组,根据解方程组,可得答案;
(3)根据互相垂直的两直线一次项的系数互为负倒数,可得PB的解析式,根据解方程组,可得P点坐标.
解答 解:(1)将(-1,-6),(2,0)代入函数解析式,得
$\left\{\begin{array}{l}{-1-b+c=-6}\\{-4+2b+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=3}\\{c=-2}\end{array}\right.$,
抛物线的解析式为y=-x2+3x-2;
(2)将抛物线C1向上平移6单位得到抛物线C2,得
y=-x2+3x+4,当x=0时,y=4,即B(0,4).
当y=0时,-x2+3x+4=0.解得x=4,x=-1,即C(-1,0),D(4,0).
BD的解析式为y=-x+4,设A′(x,y),由题意得
$\left\{\begin{array}{l}{\frac{y-m-1}{x-m}=1}\\{\frac{y+m+1}{2}=-\frac{x+m}{2}+4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=-m+3}\\{y=-m+4}\end{array}\right.$,
即A′(-m+3,-m+4).
(3)①当PB⊥BD时,设PD的解析式为y=x+b,将B点坐标代入,得
b=4,
PD的解析式为y=x+4,
联立PD与抛物线y=-x2+3x+4,
得$\left\{\begin{array}{l}{y=x+4}\\{y=-{x}^{2}+3x+4}\end{array}\right.$,
解得x=0(不符合题意,舍),x=-2,
当x=2时,y=-4+6+4=6,即P(2,6);
②当PD⊥BD时,设PD的解析式为y=x+b,将D点坐标代入,得
b=-4,
PD的解析式为y=x-4,
联立PD与抛物线y=-x2+3x+4,
$\left\{\begin{array}{l}{y=x-4}\\{y=-{x}^{2}+3x+4}\end{array}\right.$,解得x=4(不符合题意,舍),x=-2,
当x=-2时,y=-4-6+4=-6,即P′(-2,-6).
综上所述:在抛物线C2上存在点P,使△PBD是以BD为直角边的直角三角形,点P的坐标(2,6),(-2,-6).
点评 本题考查了二次函数综合题,利用待定系数法求函数解析式,利用对称点的中点在对称轴的直线上,对称点的直线的一次项系数与对称轴的一次项的系数互为负倒数得出方程组是解题关键;利用互相垂直的两直线一次项的系数互为负倒数得出PB的解析式是解题关键,要分类讨论,以防遗漏.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知线段AB
如图,已知线段AB查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
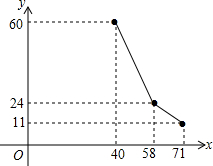 国家为支持大学生创业,提供小额无息贷款,学生王芳享受政策无息贷款36000元用来代理品牌服装的销售.已知该品牌服装进价每件40元,日销售y(件)与销售价x (元/件)之间的关系如图所示(实线),每天付员工的工资每人每天82元,每天应支付其它费用106元.
国家为支持大学生创业,提供小额无息贷款,学生王芳享受政策无息贷款36000元用来代理品牌服装的销售.已知该品牌服装进价每件40元,日销售y(件)与销售价x (元/件)之间的关系如图所示(实线),每天付员工的工资每人每天82元,每天应支付其它费用106元.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com