
 ����Ϊ֧�ִ�ѧ����ҵ���ṩС����Ϣ���ѧ����������������Ϣ����36000Ԫ��������Ʒ�Ʒ�װ�����ۣ���֪��Ʒ�Ʒ�װ����ÿ��40Ԫ��������y�����������ۼ�x ��Ԫ/����֮��Ĺ�ϵ��ͼ��ʾ��ʵ�ߣ���ÿ�츶Ա���Ĺ���ÿ��ÿ��82Ԫ��ÿ��Ӧ֧����������106Ԫ��
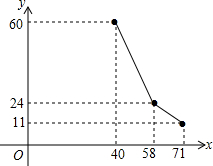
����Ϊ֧�ִ�ѧ����ҵ���ṩС����Ϣ���ѧ����������������Ϣ����36000Ԫ��������Ʒ�Ʒ�װ�����ۣ���֪��Ʒ�Ʒ�װ����ÿ��40Ԫ��������y�����������ۼ�x ��Ԫ/����֮��Ĺ�ϵ��ͼ��ʾ��ʵ�ߣ���ÿ�츶Ա���Ĺ���ÿ��ÿ��82Ԫ��ÿ��Ӧ֧����������106Ԫ������ ��1�����ݴ���ϵ�������ɵú�������ʽ��
��2�������������֧�����ɵ�һԪһ�η��̣����ݽ�һԪһ�η��̣��ɵô𰸣�
��3����������40��x��58����58��x��71���ҳ���������¶���Ϊ����ʱ��ÿ��������ߣ����ɣ�����-֧������������ծ���ɵó����ۣ�
��� �⣺��1����40��x��58ʱ����y��x�ĺ�������ʽΪy=k1x+b1����ͼ��ɵã�
$\left\{\begin{array}{l}{60=40{k}_{1}+{b}_{1}}\\{24=58{k}_{1}+{b}_{1}}\end{array}\right.$����ã�$\left\{\begin{array}{l}{{k}_{1}=-2}\\{{b}_{1}=140}\end{array}\right.$��
��y=-2x+140��
��58��x��71ʱ����y��x�ĺ�������ʽΪy=k2x+b2����ͼ��ã�
$\left\{\begin{array}{l}{24=58{k}_{2}+{b}_{2}}\\{11=71{k}_{2}+{b}_{2}}\end{array}\right.$����ã�$\left\{\begin{array}{l}{{k}_{2}=-1}\\{{b}_{2}=82}\end{array}\right.$��
��y=-x+82��
����������y=$\left\{\begin{array}{l}{-2x+140��40��x��58��}\\{-x+82��58��x��71��}\end{array}\right.$��
��2��������Ϊa����x=48ʱ��y=-2��48+140=44��
��48-40����44=106+82a��
��ã�a=3��
�𣺸õ�Ա������Ϊ3��
��3����ÿ�յ�����ΪSԪ�����У�
��40��x��58ʱ��S=��x-40����-2x+140��=-2��x-55��2+450��
�ʵ�x=55ʱ��Sȡ�����ֵ450��
��58��x��71ʱ��S=��x-40����-x+82��=-��x-61��2+441��
�ʵ�x=61ʱ��Sȡ�����ֵ441��
���Ͽ�֪����x=55ʱ��Sȡ�����ֵ450��
����Ҫb�죬�õ껹������ծ����
��450-106-82��2��b��36000��
��ã�b��200��
�ʸõ�������Ҫ200����ܻ�������ʱ��ÿ����װ�ļ۸�Ӧ��Ϊ55Ԫ��
���� ���⿼���˶��κ�����Ӧ�ã����ô���ϵ������������ʽ��һ�η��̵�Ӧ�ã�����ʽ��Ӧ�ã�����Ĺؼ��Ǹ���ͼ��������ۣ����������е��⣬�ѶȲ�����������С��������ѵ����ڣ�3���м�ֵ����ȡ����ϣ�1���Ĺ�ϵʽ�ó�ÿ������Ķ��κ�����ת��Ϊ����ʽѰ�Ҽ�ֵ��


 ֥�鿪���γ�������ϵ�д�
֥�鿪���γ�������ϵ�д� ����ѧ��ţ��Ӣ��ϵ�д�
����ѧ��ţ��Ӣ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

| �������� | ��ɽ�纣���� | ������纣���� |
| ���ų��� | 48ǧ�� | 36ǧ�� |
| ���ŷ� | 100Ԫ | 80Ԫ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
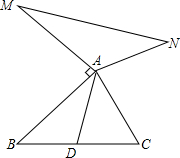 ��ͼ����֪AD�ǡ�ABC�����ߣ�AM��AB��AM=AB��AN��AC��AN=AC����֤��MN=2AD��
��ͼ����֪AD�ǡ�ABC�����ߣ�AM��AB��AM=AB��AN��AC��AN=AC����֤��MN=2AD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com