
分析 (1)根据已知数据变化规律进而得出答案;
(2)利用数据变化规律直接将原式变形进而求出答案.
解答 解:(1)①$\frac{1}{\sqrt{23}+\sqrt{22}}$=$\sqrt{23}$-$\sqrt{22}$;
②$\frac{1}{\sqrt{n}+\sqrt{n-1}}$=$\sqrt{n}$-$\sqrt{n-1}$;
故答案为:$\sqrt{23}$-$\sqrt{22}$;$\sqrt{n}$-$\sqrt{n-1}$;
(2)$\frac{1}{1+\sqrt{2}}$+$\frac{1}{\sqrt{2}+\sqrt{3}}$+$\frac{1}{\sqrt{3}+2}$+…+$\frac{1}{\sqrt{15}+4}$
=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+2-$\sqrt{3}$+…+4-$\sqrt{15}$
=-1+4
=3.
点评 此题主要考查了分母有理化,正确化简各二次根式是解题关键.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:初中数学 来源: 题型:解答题
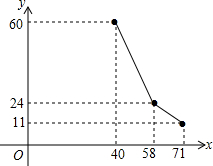 国家为支持大学生创业,提供小额无息贷款,学生王芳享受政策无息贷款36000元用来代理品牌服装的销售.已知该品牌服装进价每件40元,日销售y(件)与销售价x (元/件)之间的关系如图所示(实线),每天付员工的工资每人每天82元,每天应支付其它费用106元.
国家为支持大学生创业,提供小额无息贷款,学生王芳享受政策无息贷款36000元用来代理品牌服装的销售.已知该品牌服装进价每件40元,日销售y(件)与销售价x (元/件)之间的关系如图所示(实线),每天付员工的工资每人每天82元,每天应支付其它费用106元.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
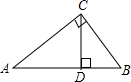 如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,互余的角是∠A与∠B、∠ACD与∠BCD、∠A与∠ACD、∠B与∠BCD;互补的角是∠ADC与∠BDC、∠ADC与∠ACB、∠ACB与∠BDC.
如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,互余的角是∠A与∠B、∠ACD与∠BCD、∠A与∠ACD、∠B与∠BCD;互补的角是∠ADC与∠BDC、∠ADC与∠ACB、∠ACB与∠BDC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
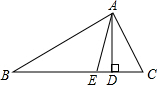 在△ABC中,∠BAC=90°,AC=5cm,AD是高,AE是斜边上的中线,且DC=$\frac{1}{2}$AC,求∠B的度数及AE的长.
在△ABC中,∠BAC=90°,AC=5cm,AD是高,AE是斜边上的中线,且DC=$\frac{1}{2}$AC,求∠B的度数及AE的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
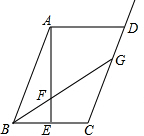 (1)探究一
(1)探究一查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com