
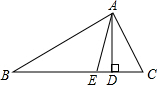
 在△ABC中,∠BAC=90°,AC=5cm,AD是高,AE是斜边上的中线,且DC=$\frac{1}{2}$AC,求∠B的度数及AE的长.
在△ABC中,∠BAC=90°,AC=5cm,AD是高,AE是斜边上的中线,且DC=$\frac{1}{2}$AC,求∠B的度数及AE的长. 分析 在RT△ACD中,由AC=2CD推出∠DAC=30°以及∠C=60°,由∠B=90°-∠C可以求出∠B,因为AE是斜边中线,所以AE=$\frac{1}{2}$BC,求出BC即可求出AE.
解答 解: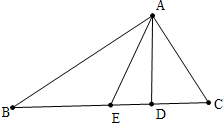 ∵AD⊥BC,
∵AD⊥BC,
∴∠ADC=90°,
∵DC=$\frac{1}{2}$AC,即AC=2CD,
∴∠DAC=30°,
∴∠C=90°-∠DAC=60°,
∵∠BAC=90°,
∴∠B=90°-∠C=30°
在RT△ABC中,∵AC=5,∠B=30°,
∴BC=2AC=10,
∵AE是中线,
∴AE=$\frac{1}{2}$AB=5.
点评 本题考查直角三角形的有关性质,本题的突破口是在直角三角形中如果斜边是直角边的两倍那么这条直角边所对的锐角为30°,属于中考常考题型.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | am与bm | B. | a2m与b2m | C. | am与-bm | D. | a2m与-b2m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.5×10-5 | B. | 3.5×10-4 | C. | 0.35×10-4 | D. | 3.5×10-6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com