
����Ŀ����ͼ��Ҫ���һ���������εĻ�̳����̳�ϵ׳�120�ף��µ׳�180�ף����µ����80�ף��������е�����(����)����һ�������������µ�֮���������������������Ŀ�����ȣ������Ŀ�Ϊx�ף�
(1)�ú�x��ʽ�ӱ�ʾ�������������
(2)������Ƶ�Ҫ�����Ŀ����ܳ���6�ף�����������ܷ���(��Ԫ)�����Ŀ��ȳ���������ϵ������ϵ����5.7����̳���ಿ�ֵ��̻�����Ϊÿƽ����0.02��Ԫ����ô�����Ŀ���Ϊ������ʱ��������̳���ܷ���Ϊ239��Ԫ��
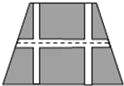
���𰸡�(1)150x��(2)�����Ŀ���Ϊ2.5��ʱ��������̳���ܷ���Ϊ239��Ԫ.
��������
��1����������ó������������Ϊ![]() ��120+180��x�������ɣ�
��120+180��x�������ɣ�
��2����̳�ܷ���y=���ܷ���+�̻��ܷ��ã�239=5.7x+��12000-S����0.02�����������
(1)��������=![]() (120+180)x=150x��
(120+180)x=150x��
(2)�������ΪS=150x+160x��2x2=310x��2x2��
�̻������Ϊ: =![]() (120+180)80-S=12000��S
(120+180)80-S=12000��S
��̳�ܷ���:y=���ܷ���+�̻��ܷ���=239
239=5.7x+(12000��S)��0.02��
239=5.7x��0.02S+240��
239=5.7x��0.02(310x��2x2)+240��
239=0.04x2��0.5x+240��
0.04x2��0.5x+1=0��
4x2��50x+100=0��
x1=2.5����x2=10
�����Ŀ����ܳ���6�ף���x��6��
��x=2.5��
��x=2.5ʱ��������̳���ܷ���Ϊ239��Ԫ��
�����Ŀ���Ϊ2.5��ʱ��������̳���ܷ���Ϊ239��Ԫ


 �����Ƹ���ʦ����ϵ�д�
�����Ƹ���ʦ����ϵ�д� ��ͨ����ͬ����ϰ��ϵ�д�
��ͨ����ͬ����ϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������ͬѧ��һ����Ϸ����һ�������Ŀڴ���װ�б�ŷֱ�Ϊ1��2��3��4���ĸ�С��(�����������������).�ӿڴ����������һ��С���±�ź�Żؿڴ��У����ҡ�Ⱥ��ٴӿڴ����������һ��С���¸�С��ı�ţ����μ��µı�ŷֱ���x��y��ʾ.��x��yΪ���������ʤ����x��yΪż�������һ�ʤ.
(1)���б�������״ͼ��(��״ͼҲ������ͼ)�е�һ�ַ�������(x��y)���п��ܳ��ֵĽ��������
(2)����Ϊ�����Ϸ��˫����ƽ����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�����![]() �Ķ�������Ϊ
�Ķ�������Ϊ![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��
��1����ͼ��1����˫����![]() ����
����![]() ��ֱ��д����
��ֱ��д����![]() �������˫���ߵĽ���ʽ��
�������˫���ߵĽ���ʽ��
��2����ͼ��2����˫����![]() ��
��![]() �ֱ��ڵ�
�ֱ��ڵ�![]() ����
����![]() ����
����![]() �ĶԳƵ�
�ĶԳƵ�![]() ��
��![]() ���ϣ���֤
���ϣ���֤![]() �������
�������![]() �����ꣻ
�����ꣻ
��3����ͼ��3����������![]() ����ƽ��
����ƽ��![]() ����λ���ȣ�ʹ����
����λ���ȣ�ʹ����![]() ��˫����
��˫����![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() Ϊ����������ʱ����
Ϊ����������ʱ����![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����κ���![]() (aΪ����)��
(a����)��
(1)��д���ö��κ���ͼ����������ʣ�
(2)��ͬһֱ������ϵ�У����ö��κ�����ͼ����![]() �IJ�����һ�κ���
�IJ�����һ�κ���![]() ��ͼ�����������㣬��
��ͼ�����������㣬��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���![]() ��ͼ���뷴��������
��ͼ���뷴��������![]() ��ͼ����
��ͼ����![]() ��B���㣬��x�ύ�ڵ�C����y�ύ�ڵ�E������
��B���㣬��x�ύ�ڵ�C����y�ύ�ڵ�E������![]() ��
��
![]() ���һ�κ����ͷ����������Ľ���ʽ��
���һ�κ����ͷ����������Ľ���ʽ��
![]() ����D��x����������һ�㣬��
����D��x����������һ�㣬��![]() ������OB��BD����
������OB��BD����![]() �������
�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() �����߶�
�����߶�![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת90���õ��߶�
˳ʱ����ת90���õ��߶�![]() ������������
������������![]() ��ͼ����
��ͼ����![]() ��
��

��1����ֱ��![]() �ͷ���������
�ͷ���������![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����֪��![]() �Ƿ���������
�Ƿ���������![]() ͼ���ϵ�һ�����㣬���
ͼ���ϵ�һ�����㣬���![]() ��ֱ��
��ֱ��![]() �������ʱ�����꣮
�������ʱ�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
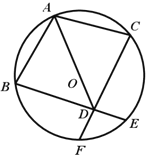
����Ŀ����֪����ͼ��AB��AC�ǡ�O�������ң���AB��AC��D��AO�ӳ�����һ�㣬����BD���ӳ�����O�ڵ�E������CD���ӳ�����O�ڵ�F.
��1����֤��BD��CD��
��2�����AB2��AO��AD����֤���ı���ABDC������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
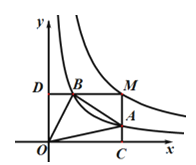
����Ŀ������������![]() ,aΪ��������
,aΪ��������![]() �ڵ�һ�����ڵ�ͼ��������ͼ��ʾ����M��
�ڵ�һ�����ڵ�ͼ��������ͼ��ʾ����M��![]() ��ͼ���ϣ�MC��x���ڵ�C����
��ͼ���ϣ�MC��x���ڵ�C����![]() ��ͼ���ڵ�A��MD��y���ڵ�D����
��ͼ���ڵ�A��MD��y���ڵ�D����![]() ��ͼ���ڵ�B����
��ͼ���ڵ�B����![]() ����
����![]() = _____________.
= _____________.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com