
【题目】如图,双曲线y=![]() 经过点A(1,2),过点A作y轴的垂线,垂足为B,交双曲线y=﹣
经过点A(1,2),过点A作y轴的垂线,垂足为B,交双曲线y=﹣![]() 于点C,直线y=m(m≠0)分别交双曲线y=﹣
于点C,直线y=m(m≠0)分别交双曲线y=﹣![]() 、y=
、y=![]() 于点P、Q.
于点P、Q.
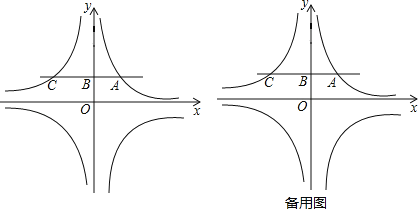
(1)求k的值;
(2)若△OAP为直角三角形,求点P的坐标;
(3)△OCQ的面积记为S△OCQ,△OAP的面积记为S△OAP,试比较S△OCQ与S△OAP的大小(直接写出结论).
【答案】(1)2;(2)见解析;(3)见解析
【解析】
试题分析:(1)直接把点A(1,2)代入双曲线y=![]() ,求出k的值即可;
,求出k的值即可;
(2)设P(﹣![]() ,m),再分∠AOP=90°,∠OAP=90°及∠APO=90°三种情况进行讨论;
,m),再分∠AOP=90°,∠OAP=90°及∠APO=90°三种情况进行讨论;
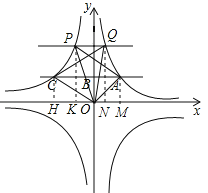
(3)根据A(1,2)可得出C(﹣9,2),设P(﹣![]() ,m),则Q(
,m),则Q(![]() ,m),分别过点A、Q、P、C作x轴的垂线,垂足分别为M、N、K、H,再由反比例函数图象上点的坐标特点得出△AOM,△QON,△COH与△POK的面积,根据S△OCQ=S梯形CHNQ﹣S△COH﹣S△POK,S△OAP=S梯形AMKP﹣S△AOM﹣S△POK即可得出结论.
,m),分别过点A、Q、P、C作x轴的垂线,垂足分别为M、N、K、H,再由反比例函数图象上点的坐标特点得出△AOM,△QON,△COH与△POK的面积,根据S△OCQ=S梯形CHNQ﹣S△COH﹣S△POK,S△OAP=S梯形AMKP﹣S△AOM﹣S△POK即可得出结论.
解:(1)∵双曲线y=![]() 经过点A(1,2),
经过点A(1,2),
∴k=1×2=2;
(2)设P(﹣![]() ,m),
,m),
∵A(1,2),
∴OA2=12+22=5,AP2=(1+![]() )2+(2﹣m)2,OP2=(
)2+(2﹣m)2,OP2=(![]() )2+m2,
)2+m2,
当∠AOP=90°时,
∵OA2+OP2=AP2,即5+(![]() )2+m2=(1+
)2+m2=(1+![]() )2+(2﹣m)2,解得m=±3,
)2+(2﹣m)2,解得m=±3,
∴P1(﹣6,3),P2(6,﹣3);
当∠OAP=90°时,
∵OA2+AP2=OP2,即5+(1+![]() )2+(2﹣m)2=(
)2+(2﹣m)2=(![]() )2+m2,解得m=
)2+m2,解得m=![]() ,
,
∴P3(![]() ,
,![]() ),P4(
),P4(![]() ,
,![]() );
);
当∠APO=90°时,此种情况不存在;
(3)∵A(1,2),
∴C(﹣9,2).
设P(﹣![]() ,m),则Q(
,m),则Q(![]() ,m),
,m),
分别过点A、Q、P、C作x轴的垂线,垂足分别为M、N、K、H,
∵点A、Q在反比例函数y=![]() 的图象上,
的图象上,
∴S△AOM=S△QON=1.
∵点C、P在反比例函数y=﹣![]() 的图象上,
的图象上,
∴S△COH=S△POK=9.
S△OCQ=S梯形CHNQ﹣S△COH﹣S△POK,S△OAP=S梯形AMKP﹣S△AOM﹣S△POK,
∴S△OCQ﹣S△OAP=S梯形CHNQ﹣S梯形AMKP,
∵梯形CHNQ与梯形AMKP的上底与下底相同,
∴只要比较HN与KM的大小即可,
∵HN﹣KM=(9+![]() )﹣(1+
)﹣(1+![]() )=8﹣
)=8﹣![]() ,
,
∴当m=±2时,HN=KM,即S△OCQ=S△OAP;
当m>2或m<﹣2时,8﹣![]() >0,即S△OCQ>S△OAP;
>0,即S△OCQ>S△OAP;
当﹣2<m<2时,8﹣![]() <0,即S△OCQ<S△OAP.
<0,即S△OCQ<S△OAP.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
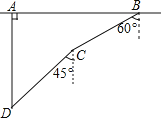
【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种服装平均每天可以销售20件,每件盈利32元,在每件降价幅度不超过10元的情况下,若每件降价1元,则每天可多售出5件,若每天要盈利900元,每件应降价 元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一列不全为零的数除了第一个数和最后一个数外,每个数都等于前后与它相邻的两数之和,则称这列数具有“波动性质”.已知一列数共有2016个,且具有“波动性质”,则这2016个数的和为( )
A.﹣64 B.0 C.18 D.64
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com