

分析 (1)证明△AMP≌△BPN,从而得到MA=PB=a,PA=NB=b,即可求出AB=PA+PB=a+b;
(2)①根据平角的定义即可求出∠MPN=60°;
②根据PM=PN以及∠MPN的度数可得到△PMN为等边三角形.利用相应的三角函数表示出MN,MP的长,可得到房间宽AB和AM长相等.
解答 解:(1)∵∠MPN=180°,
∴∠APM+∠BPN=90°,
∵∠APM+∠AMP=90°,
∴∠AMP=∠BPN.
在△AMP与△BPN中,
$\left\{\begin{array}{l}{∠AMP=∠BPN}\\{∠MAP=∠PBN=90°}\\{MP=PN}\end{array}\right.$,
∴△AMP≌△BPN,
∴MA=PB=a,PA=NB=b,
∴AB=PA+PB=a+b;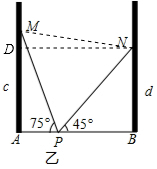 (2)①∠MPN=180°-∠APM-∠BPN=60°;
(2)①∠MPN=180°-∠APM-∠BPN=60°;
②过N点作MA垂线,垂足点D,连接NM.
设AB=x,且AB=ND=x.
∵梯子的倾斜角∠BPN为45°,
∴△BNP为等腰直角三角形,△PNM为等边三角形(180-45-75=60°,梯子长度相同),∠MND=15°.
∵∠APM=75°,
∴∠AMP=15°.
∴cos15°=$\frac{x}{MN}$=$\frac{MA}{MP}$.
∵△PNM为等边三角形,
∴NM=PM.
∴x=MA=c.
即乙房间的宽AB是c.
点评 此题考查了全等三角形的应用,解直角三角形的应用,根据PM=PN以及∠MPN的度数得到△PMN为等边三角形是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直线y=$\frac{4}{3}$x-4与x轴、y轴分别交于A、B两点,把△AOB以x轴为对称轴翻折得到△AOB′,再将△AOB′绕点A顺时针旋转90°,得到△AO′B″,则点B″的坐标是( )
如图,直线y=$\frac{4}{3}$x-4与x轴、y轴分别交于A、B两点,把△AOB以x轴为对称轴翻折得到△AOB′,再将△AOB′绕点A顺时针旋转90°,得到△AO′B″,则点B″的坐标是( )| A. | (3,4) | B. | (4,4) | C. | (7,3) | D. | (7,4) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com