
 已知直线AB的解析式为:y=$\frac{4}{3}$x+4交x轴于点A,交y轴于点B.动点C从A点出发,以每秒2个单位的速度沿x轴正方向运动,设运动时间为t.
已知直线AB的解析式为:y=$\frac{4}{3}$x+4交x轴于点A,交y轴于点B.动点C从A点出发,以每秒2个单位的速度沿x轴正方向运动,设运动时间为t.分析 (1)根据坐标轴上点的坐标特征进行计算即可;
(2)根据关于y轴对称的点的特征,求出点A关于y轴点对称点为A′的坐标,运用待定系数法求出直线BC的解析式;
(3)分点P在第三象限和第一象限两种情况,根据三角形的面积公式计算即可.
解答 解:(1)令x=0,则y=4,
∴点B(0,4),
令y=0,则$\frac{4}{3}x+4=0$,
解得:x=-3,
∴点A(-3,0);
(2)点A关于y轴点对称点为A′(3,0),
所以当点C运动到A′(3,0)时,直线BC与直线AB关于y轴对称,
则$t=\frac{6}{2}=3$秒,
设此时直线BC的解析式为:y=kx+b.
把点C(3,0)和点B(0,4)代入,
得:$\left\{\begin{array}{l}3k+b=0\\ b=4\end{array}\right.$,
解得:$\left\{\begin{array}{l}k=-\frac{4}{3}\\ b=4\end{array}\right.$,
∴直线BC的解析式为:$y=-\frac{4}{3}x+4$;
(3)存在,
当点P在第三象限时,设P(x,y)
∵S△BCP=2S△ABC,
∴S△ACP=S△ABC,
∴p(x,-4),
把y=-4代入到$y=\frac{4}{3}x+4$中得:$\frac{4}{3}x+4=-4$,
解得:x=-6,
∴P1(-6,-4);
当点P在第一象限时,设P(x,y),
∵S△BCP=2S△ABC,
∴S△ACP=3S△ABC,
∴p(x,12),
把y=12代入到$y=\frac{4}{3}x+4$中得:$\frac{4}{3}x+4=12$,
解得:x=6,
∴P2(6,12),
∴P1(-6,-4)或P2(6,12)时,S△BCP=2S△ABC.
点评 本题考查的是一次函数知识的综合运用,掌握待定系数法求一次函数的解析式、坐标轴上点的坐标特征、关于y轴对称的点的特征是解题的关键,注意分情况讨论思想的灵活运用.


科目:初中数学 来源: 题型:解答题
 2015年全球葵花籽产量约为4200万吨,比2014年上涨2.1%,某企业加工并销售葵花籽,假设销售量与加工量相等,在图中,线段AB、折线CDB分别表示葵花籽每千克的加工成本y1(元)、销售价y2(元)与产量x(kg)之间的函数关系;
2015年全球葵花籽产量约为4200万吨,比2014年上涨2.1%,某企业加工并销售葵花籽,假设销售量与加工量相等,在图中,线段AB、折线CDB分别表示葵花籽每千克的加工成本y1(元)、销售价y2(元)与产量x(kg)之间的函数关系;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在数轴上有两点A、B,A表示的数为6,B在A的左侧,且AB=10.动点P从点A出发,以每秒4个单位长度的速度沿数轴向左匀速运动.
如图,在数轴上有两点A、B,A表示的数为6,B在A的左侧,且AB=10.动点P从点A出发,以每秒4个单位长度的速度沿数轴向左匀速运动.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | … | -3 | -2 | 0 | 1 | 3 | 5 | … |
| y | … | 7 | 0 | -8 | -9 | -5 | 7 | … |
| A. | 7 | B. | 0 | C. | -5 | D. | -8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ($\sqrt{3}$)2=9 | B. | $\sqrt{25}$=±5 | C. | $\root{3}{-8}$=2 | D. | $\sqrt{36}$=6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
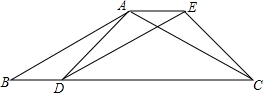 如图,已知四边形ABDE是平行四边形,C为边BD延长线上一点,连结AC、CE,使AB=AC.
如图,已知四边形ABDE是平行四边形,C为边BD延长线上一点,连结AC、CE,使AB=AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com